1) При x≤-1 - функция положительная При -1≤x≤4 - функция отрицательная При x≥4 - функция положительная выбираем те интервалы, где функция положительная (неотрицательная) - это x≤-1 и x≥4 ответ: x∈(-бесконечность; -1]U[4; +бесконечность)
2) При x≤-6 - функция положительная При -6≤x<10 - функция отрицательная При x>10 - функция положительная выбираем те интервалы, где функция положительная (неотрицательная): x∈(-бесконечность; -6]U(10; +бесконечность)
3) подкоренное выражение должно быть неотрицательным: -1≤x≤4/3
1) При x≤-1 - функция положительная При -1≤x≤4 - функция отрицательная При x≥4 - функция положительная выбираем те интервалы, где функция положительная (неотрицательная) - это x≤-1 и x≥4 ответ: x∈(-бесконечность; -1]U[4; +бесконечность)
2) При x≤-6 - функция положительная При -6≤x<10 - функция отрицательная При x>10 - функция положительная выбираем те интервалы, где функция положительная (неотрицательная): x∈(-бесконечность; -6]U(10; +бесконечность)
3) подкоренное выражение должно быть неотрицательным: -1≤x≤4/3
(5;1),(-5;1),(5;-1),(-5;-1)
Объяснение:
⁺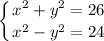
x=±5
Подставим х и найдём у
y==±1