Линейная функция имеет вид . Раз известно, что точка А(1,5; -2) принадлежит графику, и учитывая то, что координаты точки задаются как (x;y), мы можем найти коэффициент b. У нас k=1/2 по условию. Далее мы вместо y подставляем -2, а вместо x -> 1,5.
-2=(1/2)*1,5+b;
b=-2-0,75=-2,75.
Теперь у нас изветстно всё, чтобы записать уравнение графика.
.
У параллельных прямых угловой коэффициент одинаковый.
Уравнение параллельной прямой для данной будет иметь вид:
Так же подставляем вместо x и y координаты точки, чтобы найти b . Уравнение прямой, проходящей через точку (0;3): .
Решение можно сократить, если помнить, что коэффициент b как раз определяет точку пересечения с осью ординат.
||x-2|-3x|=2x+2 Подмодульная функция x-2 преобразуется в нуль в точке x=2. При меньших значениях за 2 она отрицательная и положительная для x>2. На основе этого раскрываем внутренний модуль и рассматриваем равенство на каждом из интервалов. при x∈(-∞;2) x-2<0 и |-x+2-3x|=2x+2⇒|2-4x|=2x+2 Подмодульная функция равна нулю в точке x=1/2. При меньших значениях она знакоположительная, при больших – отрицательная. Раскроем модуль для x<1/2 2-4x=2x+2⇒6x=0⇒x=0∈(-∞;1/2) Следующим шагом раскрываем модуль на интервале (1/2;2) -2+4x=2x+2⇒2x=4⇒x=2∉(1/2;2) Раскроем внутренний модуль для x>2 |x-2-3x|=2x+2⇒|-2-2x|=2x+2 Подмодульная функция положительная при x<-1 и отрицательная при x>-1 раскрываем модуль на интервале (2;∞) 2+2x=2x+2⇒x∈(2;∞) итак, х∈{0;(2;∞)} .
Линейная функция имеет вид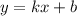
. Раз известно, что точка А(1,5; -2) принадлежит графику, и учитывая то, что координаты точки задаются как (x;y), мы можем найти коэффициент b. У нас k=1/2 по условию. Далее мы вместо y подставляем -2, а вместо x -> 1,5.
-2=(1/2)*1,5+b;
b=-2-0,75=-2,75.
.
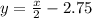Теперь у нас изветстно всё, чтобы записать уравнение графика.
У параллельных прямых угловой коэффициент одинаковый.
Уравнение параллельной прямой для данной будет иметь вид: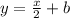
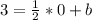
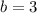. Уравнение прямой, проходящей через точку (0;3): 
.
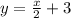Так же подставляем вместо x и y координаты точки, чтобы найти b
Решение можно сократить, если помнить, что коэффициент b как раз определяет точку пересечения с осью ординат.