Исследуйте на четность функцию :
1) y = f(x) = - 8x + x² + x³
2) y = f(x) = √(x³ + x²) - 31*| x³ |
ни четные ,ни нечетные
Объяснение:
1)
f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R
функция ни чётная ,ни нечётная
проверяем:
Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)
а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)
Как видим, f(x)≠f(-x), значит функция не является четной.
б)
f(-x) ≠ - f(-x) → функция не является нечетной
- - - - - -
2)
y = f(x) = √(x³ + x²) - 31*| x³ | ,
D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *
ООФ не симметрично относительно начало координат
* * * не определен , если x ∈ ( -∞ ; - 1) * * *
функция ни чётная ,ни нечётная
См. Объяснения
Объяснение:
№ 7
Чтобы перейти от масштаба 1:100 к масштабу 1:200, надо все размеры на карте уменьшить в 200:100 = 2 раза; соответственно размеры той же детской площадки на карте с масштабом 1:200 будут:
4 : 2 = 2 см
6 : 2 = 3 см
ответ: А) 2см х 3 см
№ 8
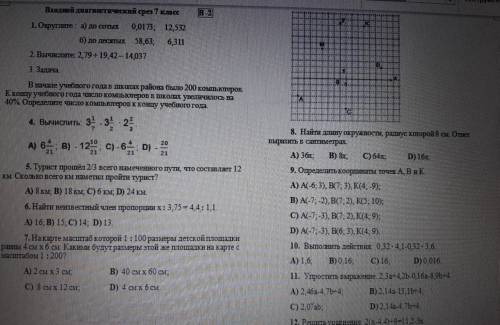
На приведённом графике находим координаты точек:
А: х = -7, у= -3
В: х = 7, у = 2
К: х = 4, у = 9.
Точки с такими же координатами даны в варианте ответа С)
ответ: С) А(-7; -3), В(7; 2), К(4; 9)
№ 9
Длина окружности С равна произведению радиуса окружности R на 2π, где π ≈ 3,14.
С = 2πR = 2π·8= 16 π см, что соответстветствует варианту ответа D).
Тот же ответ можно записать иначе:
16 π ≈ 16 · 3,14 ≈ 50,24 см
ответ: 16 π см ≈ 50,24 см