
Вариантов решение, собственно, несколько, но вот этот, по-моему, один из самых элементарных.
Рассмотрим первые три члена последовательности: а1=12; а2=10; а3=8. Очевидно, что они отвечают определнию арифметической прогрессии с разностью d=-2. Следовательно, остальные члены представляют собой другие члены прогрессии.
И при этом мы знаем, что сумма n первых членов арифметической прогрессии вычисляется по формуле Sn=0.5(a1+an)*n
а1=12; а10=-6, n=10, ну и всё, подставляем в формулу: S10=0.5(12-6)*10=30
ответ: 30
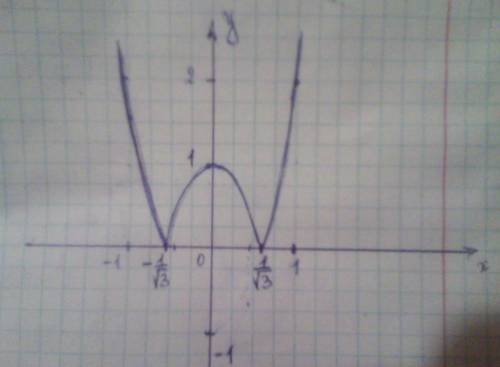
y = |(√3x - 1)(√3x + 1)|
пересечение графика функции с абциссой в точках
(√3x - 1)(√3x + 1)=0, т.е. x = -1/√3 и x = 1/√3
1 случай - модуль раскрывается со знаком +
3x² - 1 ≥ 0, x∈(-∞, -1/√3]∨[1/√3, ∞)
y = 3x² - 1 - парабола, ветви направлены вверх, вершина параболы в точке (0, -1)
Рисуем часть параболы на указанном промежутке
2 случай - модуль раскрывается со знаком -
3x² - 1 < 0, x∈[-1/√3, 1/√3]
y = -3x² + 1 - парабола, ветви направлены вниз, вершина параболы в точке (0, 1)
Рисуем часть параболы на указанном промежутке
(12;14)
Объяснение:
Приложено в
фотографии