(x+7)²=25
раскроем по формуле суммы квадратов
x²+14x+49-25=0
x²+14x+24=0
решим по теореме Виета:
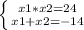 где x1, x2 - корни уравнения
где x1, x2 - корни уравнения
x1 = -12
x2 = -2
ответ: -12; -2
Объяснение: можно было бы взять корень из обоих частей, но в левой части мог появиться модуль (вроде)
2) y = 2/9
4) 2ax² - 5bx² - 4ay² + 10by² = (2a - 5b)( x - √2y)( x + √2y)
5) 3x(5-4y) + 2y(4y - 5) - 4z(15 - 12y)= (2y + 12z-3x)(4y - 5)
Объяснение:
2) (2.5y-2)(2y+2) = (10y-1)(0.5y-3) раскроим скобки:
5y² + 5y - 4y - 4 = 5y² - 30y - 0.5y +3 сгруппируем и перенесем в одну сторону:
31.5y - 7 = 0 ⇔ y = 7 / 31.5 ⇔ y = 14/63 = 2/9
4) 2ax² - 5bx² - 4ay² + 10by² = (2a - 5b)x² - 2(2a - 5b)y² = (2a - 5b)( x² - 2y²) = (2a - 5b)( x - √2y)( x + √2y)
5) 3x(5-4y) + 2y(4y - 5) - 4z(15 - 12y)= -3x(4y - 5) + 2y(4y - 5) + 4*3z(4y - 5)=
(2y + 12z-3x)(4y - 5)
(a + b)² = a² + 2ab + b² - сумма квадратов
(х + 7)² = 25
х² + 2 · х · 7 + 7² = 25
х² + 14х + 49 - 25 = 0
х² + 14х + 24 = 0
D = b² - 4ac = 14² - 4 · 1 · 24 = 196 - 96 = 100
√D = √100 = 10
х = (-b±√D)/(2a)
х₁ = (-14-10)/(2·1) = (-24)/2 = -12
х₂ = (-14+10)/(2·1) = (-4)/2 = -2
ответ: (-12; -2).