1) 
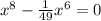
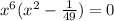
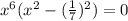
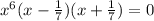
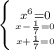
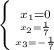
ответ: {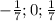 
}
2) Пусть 
(км/ч) - скорость теплохода по течению;
(км/ч) -скорость теплохода против течения, тогда
ОДЗ: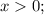 
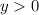
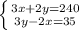
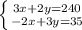
умножим первое уравнение на 2, а второе на 3:
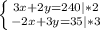
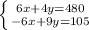
сложим:
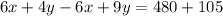
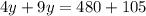
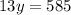
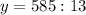
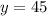
Подставим в первое и найдем :
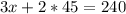
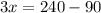
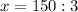
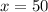
ответ: 50 км/ч - скорость теплохода по течению;
45 км/ч -скорость теплохода против течения.
3) Пусть руб. - общая сумма выигрыша, тогда
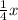руб. досталось первому;
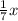руб. досталось второму;
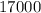руб. досталось третьему.
Уравнение:
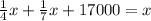
ОДЗ: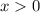 
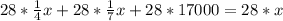
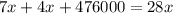
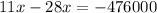
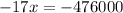
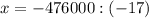
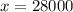руб. - общая сумма выигрыша.
Проверка:
1) 28000:4=7000 руб. досталось первому
2) 28000:7=4000 руб. досталось второму
3) 28000-(7000+4000)=17000 руб. досталось третьему.
ответ: 28 000 руб.
2. Анализ равенства показывает, что в его левой части имеется сумма двух слагаемых, каждый из которых представляет собой значение тангенс функции для различных углов. Первое слагаемое, после применения переместительного свойства сложения к его аргументу, примет вид tg(2 * π + 2 * х), а формула приведения tg(2 * π + α) = tgα позволит его записать как tg(2 * x).
3. Для преобразования второго слагаемого вспомним о периодичности тангенс функции. Как известно, тангенс функция имеет наименьший положительный период, равный π. Следовательно, из аргумента выражения tg(7 * π – 2 * x) можно отбросить 7 * π. Тогда, tg(7 * π – 2 * x) = tg(-2 * x). Наконец, учитывая нечётность тангенс функции, левая часть доказываемого равенства примет вид: tg(2 * x) + tg(–2 * x) = tg(2 * x) - tg(2 * x) = 0. Что и требовалось доказать.