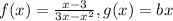
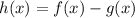 . Из определения следует, что каждый корень
. Из определения следует, что каждый корень 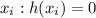 укажет координату x пересечения двух функций (то есть: для каждого корня
укажет координату x пересечения двух функций (то есть: для каждого корня 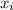 верно
верно 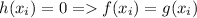 ).
).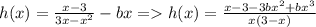
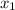 для h(x).
для h(x).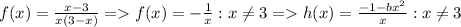
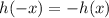 следовательно, любой корень
следовательно, любой корень 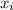 на области x>0 вернёт корень
на области x>0 вернёт корень 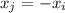 . А значит и корня будет два!
. А значит и корня будет два!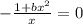 когда
когда 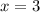 . Как было сказано раньше - мы получим (на первый взгляд) два корня
. Как было сказано раньше - мы получим (на первый взгляд) два корня 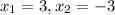 , но!
, но! 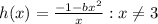 , а значит вместо
, а значит вместо 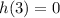 мы получаем прокол. Итого - единственный корень x=-3,
мы получаем прокол. Итого - единственный корень x=-3,
 справедливо: едиственный х выполняющий
справедливо: едиственный х выполняющий 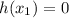 ⇒ едиственный х выполняющий
⇒ едиственный х выполняющий 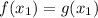 ⇒ единственная общая точка.
⇒ единственная общая точка.
ответ:а) 5x²+14x-3=0
D=b²-4ac=14²-4*5*(-3)3=196 + 60=256 (√D=16)
x₁ = = = 0,2
x₂= = = -3
Объяснение: