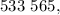 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).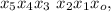


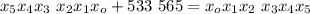 ;
;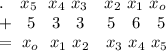

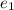 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого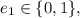
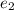 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго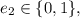
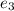 – возможная добавочная единица,
– возможная добавочная единица,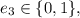
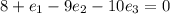 ;
;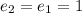 и при
и при  ;
;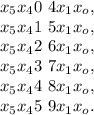
 поскольку
поскольку 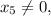 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.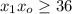 .
.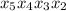 .
.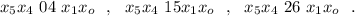
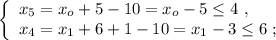

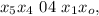
 может играть роль апреля.
может играть роль апреля.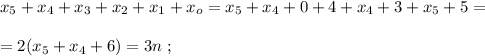
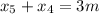 ;
;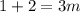 ;
;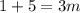 ;
;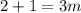 ;
; ;
;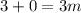 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.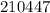 – дата 21/04/47 г.
– дата 21/04/47 г.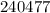 – дата 24/04/77 г.
– дата 24/04/77 г.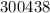 – дата 24/04/38 г.
– дата 24/04/38 г.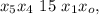
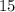 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;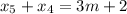 ;
;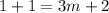 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

скорость Тига 10 км/ч.
Объяснение:
Пусть скорость Тига - х км/ч Тогда скорость Лео - (х+15) км/ч.
Тиг прибежал к финишу через 100/х ч. Лео прибежал к финишу через ((100/(х+15)) ч. Разница между финишированим бегунов - 6 ч:
100/x-100/(х+15)=6;
[100(х+15)-100x-6х(х+15)]/[x(x+15)]=0;
x(x+15)≠0;
100x+1500-100x-6x²-90=0
-6x²-90x+1500=0;
x≠0;
6x²+90x-1500=0; √D=√(8100+24*1500)=210
x₁₂=(-90±210)/12;
x₁=-300/12 <0 - не подходит;
x₂=120/12=10;
ответ: скорость Тига 10 км/ч.
Скорость Лео - 25 км/ч. Хорошо бегут (по условию они именно бегут) ребята. Быстро.