Домашняя работа 1. Преобразовать в многочлен стандартного вида
выражение:
1) (x+3)²; 2)(3y-5x)²; 3) (7-x)(7+x);
4)(4x+5y)(5y-4x); 5)(5a-0,2b)²;
6)(0,3x+0,2y)²; 7)(a+1)(a² -a+1).
2. Разложить на множители многочлен.
1)121x² - y²; 2)9x²-12xy +4y²;
1
3) - m² + 2mn + 16n ; 4)y³ +8.
16
3. Упростить выражение
(3-x)²-(x-1)(x-4)+(x-2)(x+2).
4. Решите уравнение
1) (2y-3)(3y+1)+2(y-5)(y+5)= 2(1-2y)² +6y
2) 25x² - (x + 5)² = 0.
7);
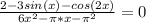
у нас производная от сложной функции, этакая "матрешка" вложение функций - брать производную просто, идем слева направо.
1. встречается sinf , f=cos^2(tg^3x) имеем y'=cos(cos^2(tg^3x))*[cos^2(tg^3x)]' самое главное - берем производную и умножаем на производную "внутренних функций."
2. квадрат косинуса [cos^2(tg^3x)]' =[2cos(cos(tg^3x))]'
3. берем производную от косинуса [2cos(cos(tg^3x))]'=-2sin[(cos(tg^3x)]
y'=cos(cos^2(tg^3x))*[2cos(cos(tg^3x))]*[-2sin[(cos(tg^3x)]*[(cos(tg^3x)]'
4. от косинуса
y'=cos(cos^2(tg^3x))*[2cos(cos(tg^3x))]*[-2sin[(cos(tg^3x)]*-sin[(tg^3x)]'
5. от tg³x (tg^3x)'=3tg²x tg'x=1/cos²x
y'=cos(cos^2(tg^3x))*[2cos(cos(tg^3x))]*[-2sin[(cos(tg^3x)]*[-sin[3tg²x]]*3tg²x
*1/cos²x