ответ: 21 см
Объяснение:
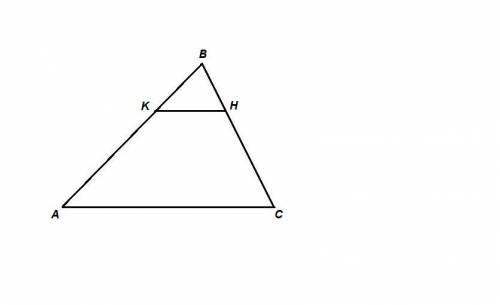
Дано: ΔАВС, КН║АС, Sakh : Sakhc = 1 : 8
Pakh = 7 см
Найти: Pabc.
Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sakh : Sakhc = 1 : 8, значит площадь треугольника АВС составляет 9 частей, тогда
Sakh : Sabc = 1 : 9 = k²
k = 1/3
Отношение периметром подобных треугольников равно коэффициенту подобия:
Pakh : Pabc = 1 : 3
Pabc = Pakh · 3 = 7 · 3 = 21 см
Площадь треугольника через стороны a , b и c.
S =√p(p-a)(p-b)(p-c) (Формула Герона) где p=(a + b+ c)/2 полупериметр.
В этой задаче p =(x+x-1+x+1)/2 =3x/2.
6√6 =√(3x/2) *(3x/2-x)*(3x/2-(x-1))*(3x/2-(x+1)) ;
6√6 =√(3x/2) *(x/2)*((x+2)/2))*((x-2)/2)) ;
36*6 =3x²(x² -4)/16 ;
36*2 =x²(x² -4)/ 16;
36*32 =x²(x² -4) ; * * * t =x² >0 ; t(t-4) =36*32* * *
---
x² =36 ⇒x =6 .
a=6 ; b=5 ; c=7.
S =a*h(a)/2 ⇒
h(a)=2S/a =(2*6√6)/6 =2√6.
h(b)=2S/a =(2*6√6)/5 =12√6/5.
h(c)=2S/a =(2*6√6)/7 =12√6/7.