Если осевое сечение конуса - равносторонний треугольник, то в конусе половина образующей равна радиусу основания. Проведем осевое сечение и получившийся треугольник обозначим ABC, где A - вершина конуса. Опустим высоту AH - которая явл. так же медианой и биссектрисой.
BH обозначим r - радиус окружности в основании конуса.
BA тогда будет 2r
Из прямоугольного треугольника ABH:
AH² = BA² - BH²
AH² = 4r² - r²
AH² = 3r²
AH = r√3
Объем конуса V = πr²h/3 (где r - радиус основания, а h - высота)
V = πBH²AH²/3 = πr²r√3/3 = πr³√3/3
Но V так же равно 36.
πr³√3/3 = 36
r³ = 36√3/π
r = ∛(36√3/π)
Вычислим радиус вписанного шара - R
Осевое сечение шара является вписанной окружностью для треугольника в осевом сечении конуса. R этой окружности и R шара - одинаковы.
Так как треугольник ABC равносторонний R = a√3/6 (а - сторона треугольника)
Сторона треугольника - 2r = 2∛(36√3/π)
R = ∛(36√3/π)*√3/6
Vшар = 4πR³/3
Vшар = 4π(∛(36√3/π)*√3/6)³/3 = (4π(36√3/π)*3√3/36*6)/3 = 4*36√3*3√3/36*6*3 = 4/2 = 2
ответ: 2
Воспользуемся формулой 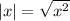 :
:
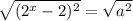
Возведем обе части в квадрат:
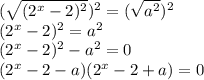
Рассмотрим 3 случая :
1.
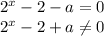
----------------------
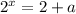
Мы знаем, что любое число(кроме 0) в любой степени больше нуля, то есть 2+а > 0 => a>-2
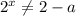
Так же 2-а уже должно быть меньше или равно нулю:
2-a ≤ 0 => a ≥ 2
Найдем пересечение => a ≥ 2
2.
По тому же принципу :
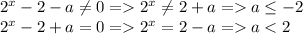
Найдем пересечение => a ≤-2
3.
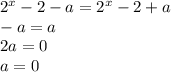
----------------------------------------------------------------------
Объединим три ответа => a Є (-∞ ; -2] U [2 ; +∞)
ответ : a Є (-∞ ; -2] U [2 ; +∞) U {0}
P.S это одно из возможных решений, возможно вы найдете и по проще)
Объяснение:
n∈Z