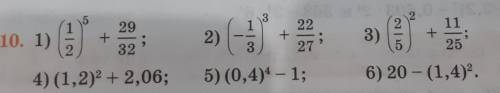
чтобы наибольшее значение данной функции было не меньше 1, необходимо и достаточно, чтобы она в какой-то точке приняла значение 1.
если наибольшее значение функции не меньше единицы, то по непрерывности в какой-то точке будет значение единица. если же наибольшее значение меньше единицы, то значение единица приниматься не может. значит нужно найти при каких значениях a есть корни у уравнения |x - a| = x² + 1
так как x² + 1 > 0 , то уравнение равносильно совокупности :
эта совокупность имеет решение, если:
Объяснение:
1)(½)⁵+29/32= 1/32+29/32=30/32=15/16
2)(-⅓)³+22/27= -1/27+22/27=21/27= 7/9
3)(⅖)²+11/25= 4/25+11/25=15/25=3/5 или 0.6
4)(1.2)²+2.06=1.44+2.06=3.5
5)(0.4)⁴-1= (⅖)⁴-1= 16/625-1=-609/625
6)20-(1.4)²=20-1.96=18.04