Четные числа отличаются друг от друга на 2; например, 4, 6 и 8 или 12, 14 и 16.
Пусть 1-е число - х, тогда 2-е число - (х + 2), а 3-е число - (х + 4). Составим и решим уравнение по условию задачи:
х² + (х + 2)² = (х + 4)²,
х² + х² + 4х + 4 = х² + 8х + 16,
2х² + 4х + 4 = х² + 8х + 16,
2х² + 4х + 4 - х² - 8х - 16 = 0,
х² - 4х - 12 = 0.
D = (-4)² - 4 · 1 · (-12) = 16 + 48 = 64; √64 = 8.
х₁ = (4 + 8) / (2 · 1) = 12 / 2 = 6, х₂ = (4 - 8) / (2 · 1) = -4 / 2 = -2.
Значит, три четных числа - это числа 6, 8 и 10 или -2, 0 и 2.
ответ: 6, 8 и 10 или -2, 0 и 2.
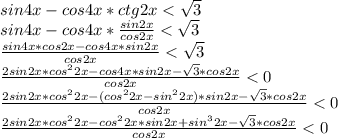
Для удобства для начала отдельно рассмотрю числитель
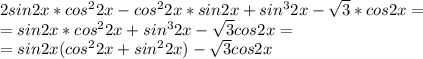
Заметим, что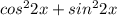 
равно одному, это главное тригоном. тождество,
напомню, что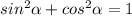 
, только в нашем случае α=2x
Заменяем на единицу и все упрощается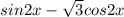
И так получили следущее
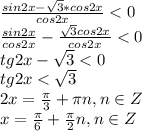
При этом
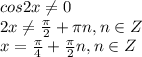
У нас получилось две серии корней, с периодами пи/2. поэтому на на круге будет очень много корней. Не знаю так знадумывалось ли, но придётся проверять знаки на промежутках между этими корнями. В итоге на круге будет 8 корней. Некоторая переодичность в знакопостоянстве улавливается, но не сразу и она не однозначна.
Нам нужно <0.
И выходит:
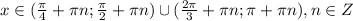
x, y = 1,3
Объяснение:
45x - 9y + 6x+4y = 36
6x+2y - 3x +9y = 36
51x-5y=36 /11
3x+11y=36 /5 и прибавляем
x= 1
y= 3