Сократить дробь
н в квадрате-64(числитель)
5н+40(знаменатель) =
очень

👇

Увидеть ответ

Ответ:

valeriyait

06.11.2020

(n²-64)/(5n-40)=(n-8)(n+8)/5(n+8)=(n-8)/5

4,8(12 оценок)

Открыть все ответы

Ответ:

Глеб0417

06.11.2020

Нужно использовать следующие свойства числовых неравенств:

1. К обеим частям верного числового неравенства можно прибавить одно и то же число и получится верное числовое неравенство, т.е.:

если а < b и с - любое число, то a + c < b + c.

2. Обе части верного числового неравенства можно умножить (разделить) на одно и то же положительное число, при этом получиться верное числовое неравенство; если же число отрицательное, то знак неравенства изменится на противоположный, т.е.:

если а < b и с > 0, то ac < bc;

если а < b и с < 0, то ac >bc.

Таким образом, если а < b, то: 2,5а < 2,5b (2,5 > 0),

а затем и 2,5а - 7 < 2,5b - 7.

ответ: 2,5а - 7 < 2,5b - 7.

4,5(92 оценок)

Ответ:

Danfdffefd

06.11.2020

Исходное неравенство распадается на совокупность систем:

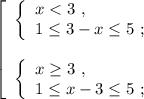
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

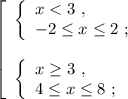
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

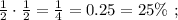
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

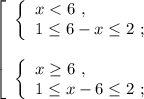
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

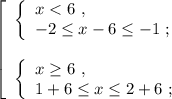
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

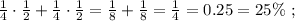
Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Это интересно:

Компьютеры-и-электроника

22.03.2021

Как выйти из учетной записи Google на Android–устройстве?...

Мир-работы

10.09.2022

Как стать зеленым беретом: все, что вы хотели знать о вступлении в элитное подразделение армии...

Компьютеры-и-электроника

19.07.2021

Как контролировать контент на YouTube с помощью блокирования по ключевым словам?...

Образование-и-коммуникации