Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 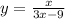 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)  при
при 
Если x = -5, то 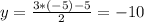
Если х= 3, то 
Значит, 
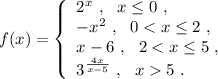
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
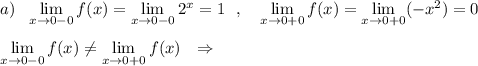
При х=0 функция имеет разрыв 1 рода .
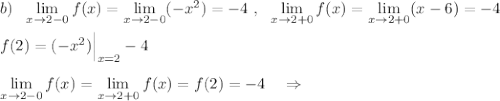
При х=2 функция непрерывна.
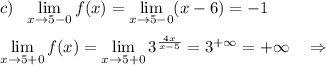
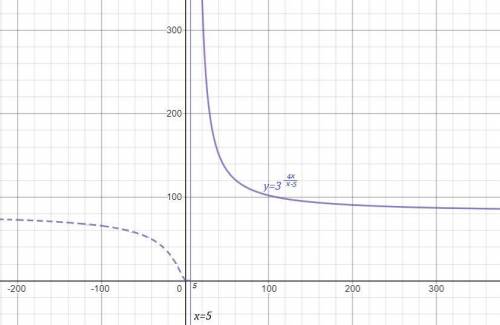
При х=5 функция имеет разрыв 2 рода .
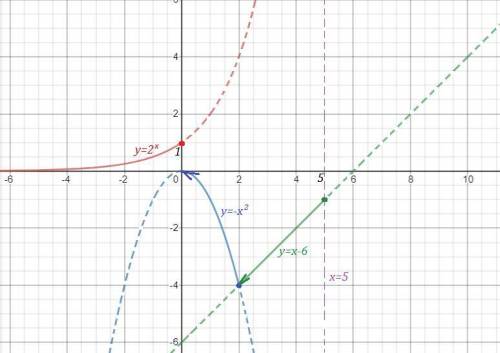
График функции нарисован сплошной линией.
На 1 рисунке нет чертежа функции 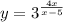 при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
раскрываем скобки
это квадратное уравнение, поэтому переносим всё влево
для удобства можно сократить уравнение на –4, чтобы избавиться от минусов. Можно и оставить так, как есть
Готово. Квадратное уравнение. Решаем через дискриминант
D < 0, значит корней уравнения нет.
ответ: уравнение не имеет решений.