Какие допустимые значения переменной являются допустимыми, а какие недопустимыми для данного выражения:

Question

Алгебра: Какие допустимые значения переменной являются допустимыми, а какие недопустимыми для данного выражения:

succura · Accepted Answer

Извлечь квадратный корень из обеих частей неравенства:

|5x-8|≥|8x-5|;

Переместить выражение в левую часть и изменить его знак:

|5x-8|-|8x-5|≥0;

Разделить неравенство на 4 возможных случая:

5x-8-(8x-5)≥0, 5x-8≥0, 8x-5≥0

-(5x-8)-(8x-5)≥0, 5x-8<0, 8x-5≥0

5x-8-(-(8x-5))≥0, 5x-8≥0, 8x-5<0

-(5x-8)-(-(8x-5))≥0, 5x-8<0, 8x-5<0;

Решить неравенство относительно x:

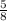
x≤-1, x≥ $\frac{8}{5}$ , x≥ $\frac{5}{8}$

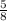
x≤1, x< $\frac{8}{5}$ , x≥ $\frac{5}{8}$

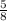
x≥1, x≥ $\frac{8}{5}$ , x< $\frac{5}{8}$

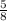x≥-1, x< $\frac{8}{5}$ , x< $\frac{5}{8}$ ;

Найти пересечение:

x≤-1, x∈[ $\frac{8}{5}$ ;∞)

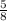x≤1, x∈[ $\frac{5}{8}$ ; $\frac{8}{5}$ )

x≥1, x∈∅

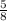x≥-1, x∈(-∞; $\frac{5}{8}$ );

Ещё раз найти пересечение:

x∈∅

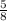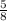x∈[ $\frac{5}{8}$ ;1]

x∈∅

x∈[-1; $\frac{5}{8}$ );

Из получившегося ответа ещё раз найти пересечение:

x∈[-1;1]