Возьмем ваше же уравнение
lx+2l+lxl+lx-2l=4
Левую и правую части уравнения рассматриваем как функции.
f(x)=lx+2l+lxl+lx-2l и g(x)=4
С g(x) все понятно. Это прямая y=4, параллельна Ox.
С f(x) разбираемся. Это кусочная функция. Найдем нули подмодульных выражений:
x+2=0 ⇒ x=-2, x-2=0 ⇒ x=2, x=0.
Имеем интервалы (-∞; -2); [-2; 0); [0; 2); [2; +∞). Запишем равносильный переход:
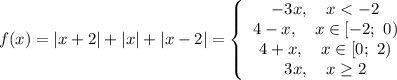
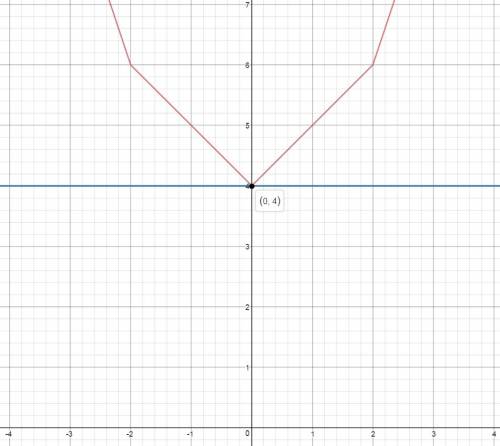
Построение графика на этом этапе элементарно. Из системы можно видеть, что функция f(x) четная. Достаточно построить или левую или правую ее часть, остальное отзеркалить. Готовый рисунок приложен.
Первая производная
f'(x) = 4·(x-5)^3·(x+2)^3+3·(x-5)^2·(x+2)^4
или
f'(x)=7·(x-5)^2·(x-2)·(x+2)^3
Находим нули функции. Для этого приравниваем производную к нулю
(x-5)^2·(x-2)·(x+2)^3 = 0
Откуда
x1 = 5
x2 = -2
x3 = 2
(-∞ ;-2),f'(x) > 0-функция возрастает
(-2; 2),f'(x) < 0-функция убывает
(2; 5),f'(x) > 0-функция возрастает
(5; +∞),f'(x) > 0-функция возрастает
В окрестности точки x = -2 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 - точка максимума. В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума.
Объяснение:
Область допустимых значений (ОДЗ) переменных — это все значения переменных (множество), при которых выражение имеет смысл.
Алгоритм:
1. выписываем все знаменатели
2. находим, при каком значении переменной знаменатель равен 0.
3. решаем полученные уравнения.
4. в ответ пишем все значения переменной, кроме полученных в п. 3
Выражение: (4 + х²) / ( 5 - х)
Знаменатель: 5 - х → 5 - х ≠ 0 → х ≠ 5
Выражение имеет смысл при всех х, кроме х =5.
ОДЗ: Так как число «−5» не входит в область определения функции, при записи ответа рядом с ним будет стоять круглая скобка
(- ∞; 5) ∪ (5; +∞)
72 / 6(х² - 4) → 6(х² - 4) ≠0 → х² - 4 ≠ 0 → (х - 2)(х+2) ≠ 0, откуда
х ≠2; х ≠ -2
2) Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа.
√х → ОДЗ: х ≥ 0
(-∞; -2) ∪ (-2; 2) ∪(2; + ∞), т.е в ОДЗ входят все значения от -∞ до -2, от -2 до 2 (при этом -2 и 2 не входят, и от 2 до +∞)