Question

2 1.3. Выполните возведение в степень: 1)
в 2 степени;

3)
2)
в 5 степени
4) 0,3 в 3 степени;
5)0,1 в 3 степени
6)(1 1/2) в 4 степени
7) на фото

$( \frac{1}{2} )$
$( - \frac{2}{3})^{2}$
$( - \frac{1}{2})$

Answer 1

1. 0,25

2.-32 вниз 1 сверху

3. -9 вниз 4 сверху

4. 0.27

5.0.001

6.сверху9 вниз 4

7. сверху 27 вниз64

Answer 2

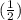
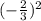
Объяснение:

1) (1/2)²=1/4=0,25

2))(- ½)^5=-1/32 3)(- 2/3)²= 4/9 4) 0,3³=0,027

5) 0,1³=0,001 6) ( 1 ½)^4=(3/2)^4=81/16 =5 1/16 7) (- ¾)³=-27/64

8) (2 ½)³= (5/2)³=125/8=15 5/8

Z.1.4

1)5*5*5*5=5^4 4) a*a*b*b*b=a²b³ 7) u*u*b*b=u²b²

2)x*x*x*x*x*x=x^5 5)x*x +y*y=x² + y² 8) m*x*x + n*n*y*y*y=mx²+n²y³

3)5*5*5*a*a=5³a² 6)m*m*m+m*m=m³+m² 9) 2*x*x*z*z+y*y*y=2x²z²+y³