это если тебе будет не понятно как я написала:
2(3-5x)=4(1-x)-1
6-10x=4-4x-1
-10x+4x=4-1-6
-6x=-3|÷(-6)
x=0,41
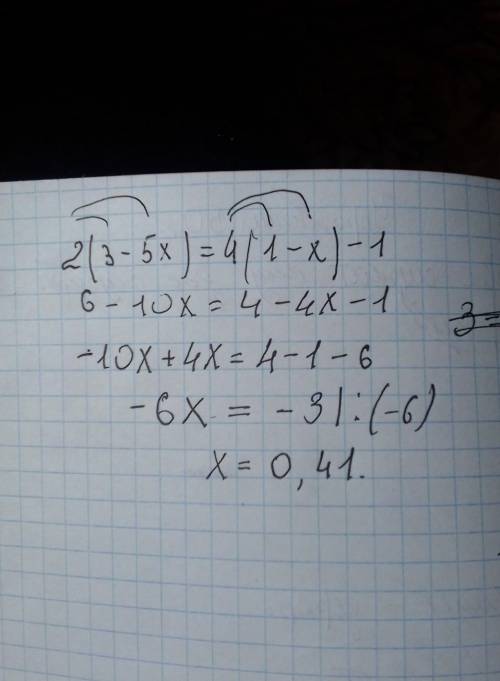
Из 9 солдат нужно выбрать некоторых 7. Число сделать это равно числу сочетаний из 9 элементов по 7:
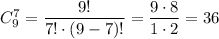
Из 6 сержантов нужно выбрать некоторых 4. Число сделать это равно числу сочетаний из 6 элементов по 4:
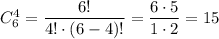
Из 4 офицеров нужно выбрать некоторого 1. Число сделать это равно числу сочетаний из 4 элементов по 1:
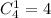
Так как выбор солдат, выбор сержантов и выбор офицера попарно независимы, то соответствующие нужны перемножить. То есть любому выбору солдат мы можем сопоставить любой выбор сержантов, а также любой выбор офицера.
Общее число вариантов:
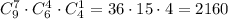
ответ: 2160 вариантов
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 2x1 + x2 - 3x3 + 5x4 = 0
{ 3x1 - 2x2 + x3 - 3x4 = 0
{ 3x1 + 5x2 - 10x3 + 18x4 = 0
Умножаем 1 уравнение на -2 и складываем со 2 уравнением.
Умножаем 1 уравнение на -3 и складываем с 3 уравнением.
Умножаем 4 уравнение на -1 и складываем с 3 уравнением.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
{ 0x1 - 14x2 + 22x3 - 42x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
2, 3 и 4 уравнения все одинаковые, от них можно оставить одно.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
Переменные x3 и x4 - свободные, могут быть какими угодно.
x2 = 11/7*x3 - 3x4
x1 = 7x3 - 13x4 - 4x2 = 7x3 - 13x4 - 44/7*x3 + 12x4 = 5/7*x3 - x4
Это общее решение системы.
Ненулевое решение: например, x3 = 7, x4 = 1, x2 = 8, x1 = 4
6-10x=4-4x-1
14x=-3
x=- 3/14