Объяснение:
Квадратное уравнение можно представить в виде:
a(x-x1)(x-x2)=0, где x1 и x2 - корни уравнения;
Раскроем скобки, тогда a*x^2-a*x(x1+x2)+a*x1*x2=0 (1)
у нас выражение x^2-x-p=0 (2)
Если сравнить 2 выражения.
Коэффициент в (2) перед x^2=1, отсюда следует, что в (1) a=1.
(1) принимает вид:
x^2-x*(x1+x2)+x1*x2=0
Сравниваем коэффициенты перед x, получаем
x1+x2=1 (3)
сравниваем свободные члены
-p=x1*x2 (4)
также по условию
x1^2+x2^2=25; (5)
тут 2 варианта, решить систему выше или можно предположить решение;
Предположим, что x1=-4, x2=5;
Тогда удовлетворяются все уравнения условия - (3), (5);
получаем, что p=-(-4)*(5)=20
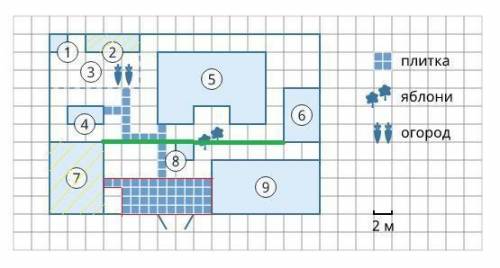
1) 5коробок 2) 60 м² 3) 20 м
Объяснение:
1) По рисунку видно, что 1 плитка 0,5*0,5 клетки, или с учетом масштаба:
0,5*0,5*2*2=1 м²
По схеме видно, что дорожка занимает 5*2 клеток и еще 0,5*1 клетку. Рассчитаем площадь плитки с учетом масштаба:
5*2*2*2+0,5*1*2*2=42 м² занимает площадь плитки от коровника к курятнику
42:1=42 плитки
42:10=4,2 коробки округляем в большую сторону до целого 5 коробок
2) Размер теплицы в клетках: 3*1
Размер коровника в клетках: 3*4
Площадь коровника и теплицы с учетом масштаба:
3*1*2*2+3*4*2*2=60 м²
3) Расстояние между двумя ближайшими точками - это расстояние от правого верхнего угла коровника до левого нижнего угла коровника.
Это 10 клеток или 10*2=20 м
2) 5(x-z)-2(x+z)=5x - 5z -2x - 2z= 3x - 7z
3) 2(2r-3s)-3(r-2s)=4r - 6s - 3r +6s= r
4) 6(2a+c)+2(6a-c)-4c= 12a+6c+12a - 2c=24a+4c
5) b(m-7)-7b=bm - 7b - 7b= bm - 14b
6) x(c+1)+c(x-1)=xc+x+xc - c= 2xc+x - c
7) y(x-4)+x(3-y)=yx - 4y+3x - yx= - 4y+3x