b1+b2+b3=112
b4+b5+b6=14
bn=b1*q^(n-1) - формула n-го члена геометрической прогрессии
=> b2 = b1*q; b3=b1*q^2; b4=b1*q^3; b5=b1*q^4; b6=b1*q^5
b1+b1q+b1q^2=112
b1q^3+b1q^4+b1q^5=14
Вынесем за скобку из первого уравнения b1: b1(1+q+q^2)=112
Вынесем за скобку из второго уравнения b1q^3: b1q^3(1+q+q^2)=14
Выразим из первого уравнения (1+q+q^2): 1+q+q^2=112/b1
Подставим во второе уравнение: b1q^3*(112/b1)=14
q^3*112=14
q^3=1/8
q=1/2
Из первого уравнения: b1=112/(1+q+q^2)=112/(1+1/2+1/4)=112/(7/4)=16*4=64
ответ: 64
Рассмотрим последние цифры степеней чисел 3 и 7 (очевидно, степени чисел 33 и 77 оканчиваются на те же цифры; в таблице последняя цифра числа x обозначена как x mod 10):

Дальше таблицу можно не продолжать: поскольку последняя цифра степени определяется только последней цифрой предыдущей степени, то дальше всё будет повторяться: например, для степеней тройки дальше идут 3, 9, 7, 1, 3, 9, ... Таким образом, последовательность последних цифр степеней тройки и семёрки является периодической с периодом 4, то есть прибавление любого количества четвёрок к показателю степени последнюю цифру не меняет.
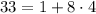 , поэтому
, поэтому 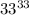 оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и  , то есть на 3.
, то есть на 3. 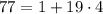 , поэтому
, поэтому  оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и  , то есть на 7. Значит, сумма
, то есть на 7. Значит, сумма  оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и 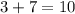 , то есть на 0. Искомый остаток равен нулю.
, то есть на 0. Искомый остаток равен нулю.
ответ. 0
Если первый образуют геометрическую прогрессию то справедливо равенство
если вторые образуют арифметическую прогрессию, то
теперь преобразуем
нам нужно найти соотношение y/x
то есть их 2 , первое это выходит постоянная прогрессия , вторая убывающая