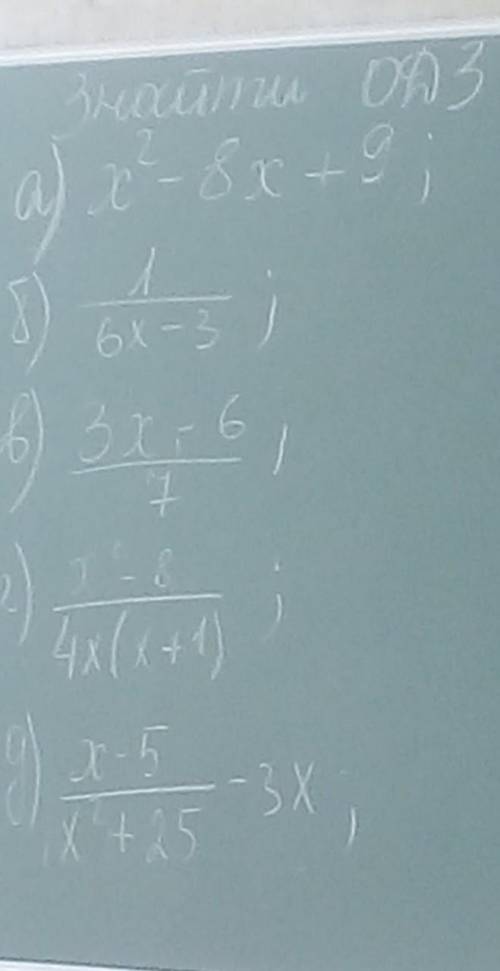
Объяснение:
1 . a ) x² - 8x + 9 ; ОДЗ : (- ∞ ; + ∞ ) ;
б) 1/( 6х - 3 ) ; ОДЗ : х ≠ 0,5 ;
в) ( 3х - 6 )/7 ; ОДЗ : (- ∞ ; + ∞ ) ;
г ) ( х - 8 )/4х( х + 1 ) ; ОДЗ : х ≠ -1 , х ≠ 0 ;
д ) ( х - 5 )/( х² + 25 ) - 3х ; ОДЗ : (- ∞ ; + ∞ ) ;
1)0.7<1
X<0.7 функция спадает меняем знак
2)1/2<1 функция спадает меняем знак
2x-1>0 решаем систему 2x>1 x>3/2
2x-1>2 2x>3
3)x2-6x+8>0 x от минус бесконечности к 2 от 4 к плюс бесконечности
X2-6x+8>2 x2-6x+6>o x от минус бесконечности к (6-sqrt(12))/2 от (6+sqrt(12))/2 к плюс бесконечности
решаем систему общие кореня x от минус бесконечности к 2 от 4 к плюс бесконечности
4) log 0,5 (2x - 4) < log 0,5 ( х + 1)
МЕТОД ПОТЕНЦИОНИРОВАНИЯ
НЕ ЗАБИВАЙТЕ ЧТО ОСНОВЫ МЕНЬШЕ 1
И ЧИСЛО ПОД ЛОГОРИФМОМ БОЛЬШЕ 0
РЕШАЕМ СИСТЕИУ
2X-4>0 X>2
x+1>0 X>-1 OТВЕТ Х>5
2X-4>X+1 X>5
БУДУТ ВОПРОСы ОБРАЩАЙТЕСЬ
V₁=V - V₀ (за V₀ примем скорость течения реки,а за v -скорость катера)-это когда он ехал против течения;
V₂=V+V₀ -скорость по течению;
V₃=V -скорость в стоячей воде;
t₁ -время против течения;
t₂ -время по течению;
Теперь вспомним формулу пути: S=V*t (где V -скорость катера,а t -его время)
По условию сказано,что по течению за 5 часов он путь на 20 км больше чем против течения за 4 часа.
Теперь подставим в формулу пути значения времени и формулу скорости(выведенную вначале).
S₁=V₁×t₁=(вместо V₁ пишем V -V₀);=(V-V₀)×4;(Время нам дано по условию)
S₂=V₂×t₂=(вместо V₂ пишем V+V₀);=(V+V₀)×5;
Получаем систему уравнений прощения, знака системы не нашёл):
(15,5-V₀)×4=S₁
(15,5+V₀)×5=S₂
Но мы знаем разницу S₂-S₁=20
И теперь вместо S₂ и S₁ подставляем в эту разницу (15,5+V₀)×5 и (15,5-V₀)×4 соответственно.
После раскрытия скобок и привидения подобных получаем: 9V₀=4,5.
Отсюда легко находим V₀. V₀= 0,5км/час
ниже
Объяснение:
Чтобы узнать ОДЗ нужно рассмотреть ситуации, когда знаменатель будет 0, так как в рамках школьной программы делить на 0 нельзя