Данная функция - квадратичная (функция, уравнение которой включает в себя переменную 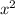 ). Стандартный вид функции:
). Стандартный вид функции: 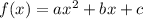 .
.
То есть в нашей функции 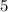 это
это  ,
, 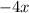 это
это 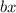 и
и 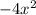 это
это 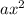 .
.
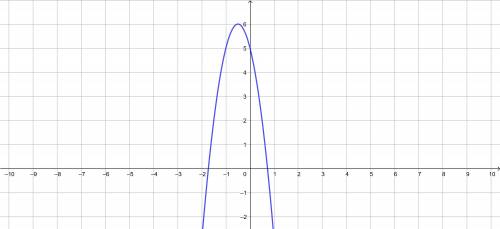
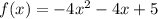 .2. Определим направление параболы.
.2. Определим направление параболы.График квадратичной функции - парабола (геометрическое место точек, равноудалённых от данной прямой). Ветви параболы могут быть направлены вверх и вниз.
Если коэффициент  при переменной
при переменной 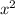 положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
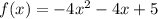 . Здесь
. Здесь 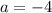 , поэтому ветви параболы направлены вниз.3. Вычислим координату
, поэтому ветви параболы направлены вниз.3. Вычислим координату  вершины параболы.
вершины параболы.Координата  вершины параболы - значение
вершины параболы - значение 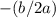 . Если квадратичная функция записана в стандартном виде
. Если квадратичная функция записана в стандартном виде 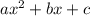 , воспользуемся коэффициентами
, воспользуемся коэффициентами  и
и 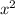 :
:
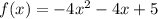 коэффициенты
коэффициенты 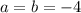 . Т.е. координата
. Т.е. координата  вершины параболы:
вершины параболы: 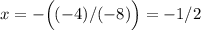 .4. Найдём соответствующее значение
.4. Найдём соответствующее значение 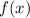 .
.Мы ищем максимум функции, так как ветви параболы направлены вниз. Чтобы найти максимум нужно подставить в исходную функцию 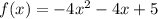 найденное значение
найденное значение  .
.
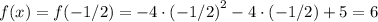 5. Запишем окончательный ответ.
5. Запишем окончательный ответ.Точка максимума функции равна 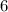 .
.
В таких случаях надо во второй дес.дроби (0,9) перенисти запятую в конец числа. Получится число 9. Так как в 0,9 после запятой стоит один знак, то и в первой дес.дроби запятую нужно перенести на один знак вперед. То есть, когда мы запятую переносим в первой дес.дроби мы смотрим на кол-во знаков после запятой во второй десятичной дроби. Получается пример: 6,3 : 0,9 = 63 : 9 = 7
Похожие примеры: 63 : 0,9 = 630 : 9 = 70
4,8 : 0,6 = 48 : 6 = 8
Так же есть другие примеры деления. Имеем пример: 4,8 : 6
В этом случае действие выполняется в столбик.
Пример решения на фото.
Мы видим, что 4 на 6 делить нельзя. Значит 6 × 0. Получается 4 плюс сносим следующее число - 8. Получается 48. 6×8=48.
На фото более подробно, словами сложно. Советуюю спросить у учителя или набрать в интернете.