Объяснение:
Задание 2.
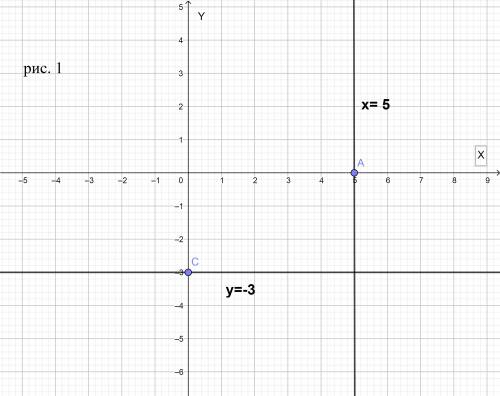
а) Координату х=5 будут иметь все точки , лежащие на прямой , которая параллельна оси ординат и проходит через т.А на оси абсцисс. Любая другая точка координатной плоскости имеет абсциссу отличную от х=5
б) Координату у=-3 будут иметь все точки , лежащие на прямой , которая параллельна оси абсцисс и проходит через т.С на оси ординат. Любая другая точка координатной плоскости имеет ординату отличную от у=-3
рисунок 1 во вложении
Задание 3.
а) На координатной плоскости неравенство х ≥ 4 задаст полуплоскость , которая будет расположена правее прямой х=4. Все точки этой полуплоскости будут иметь абсциссу равную 4 и больше
рисунок 2 во вложении
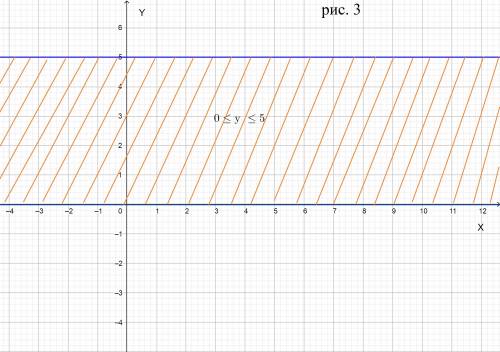
б) Двойное неравенство 0 ≤ у ≤ 5 задает на координатной плоскости две горизонтальные полосы , которые имееют ординату 0 и 5
рисунок 3 во вложении
Задание 4.
а) у = х;
найдем точки и построим график
х=0, у=0
х=3 , у=3
х=-3, у= -3
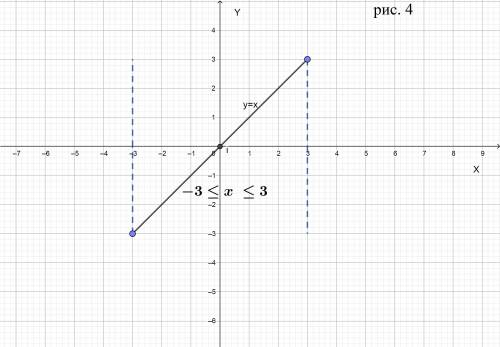
б) –3 ≤ х ≤ 3.
неравенство задает на координатной плоскости две вертикальные полосы, которые имею абсциссу 3 и -3
Изобразим множество точек на координатной плоскости
рисунок 4 во вложении
Задание 5
Решение во вложении
Задание 6
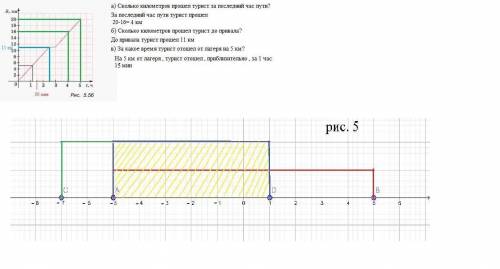
Если | x | ≤ 5 , значит -5 ≤ х ≤ 5, т.е. х ϵ [-5 ; 5]
Отметим этот промежуток т.А и т.В на координатной прямой ( рис. 5 во вложении)
Отметим промежуток –7 ≤ x ≤ 1 , т.е. х ϵ [ -7 ; 1] на координатной прямой т.С и т. D
Для того, чтобы определить границы промежутков [-5; 5] и [-7; 1] сравним левые и правые границы этих промежутков. Поскольку -7 < -5, а 5 >1 , то искомое пересечение имеет вид: х ϵ[-5; 1]

ОбъяснеРешить методом Гаусса
3х+2у+z=2
2х-5у+3z=-13
2x-3y+5z=-3
Решение
Поменяем местами первое и третье уравнение
Первое уравнение разделим на 2
от 2го и 3го уравнения отнимаем 1ое уравнение, умноженное соответственно на 2; 3
₋ 2x - 5y + 3z = -13
2x - 3y + 5z = -3
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
- 2y - 2z = -10
y + z = 5
₋ 3x + 2y + z = 2
3x - 4,5y + 7,5z = -4,5
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
6,5y - 6,5z = 6,5
y - z = 1
Получим систему уравнений
от 3 уравнения отнимаем 2 уравнение
₋ y - z = 1
y + z = 5
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
-2z = -4
z = 2
Получили систему уравнений
Прямой ход решения по методу Гаусса закончили.
Теперь обратный ход решения позволит найти переменные х и у.
От 1го и 2го уравнений отнимаем 3 уравнение, умноженное соответственно на 2,5 и 1
₋ x - 1,5y + 2,5z = -1,5
2,5z = 5
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
x - 1,5y = -6,5
y + z = 5
z = 2
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
y = 3
Получили систему уравнений
От 1го уравнения отнимаем 2ое уравнение, умноженное на -1,5
₋ x - 1,5y = -6,5
- 1,5y = -4,5
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
x = -2
Получили систему уравнений
ние:
Объяснение:
_1_
1) 3*(5х + 9у – z)=3*5x+3*9y-3*z=15x+27y-3z;
2) –6*(–а – 9b + 7с)=-6*(-a)-6*(-9b)-6*(7c)=6a+54b-42c;
3) (6р – n – 4m) * (–1,6)=(–1,6)*6p-(–1,6)*n-(–1,6)*4m=-9,6p+1,6n+6,4m;
4) (–2,6а – b + 1,4с) * (–m)= (–m)*(-2,6a)- (–m)*b+ (–m)*1,4c=2,6am+bm-1,4cm;
5) –0,7n*(7а – 2,1 + 5k)=(–0,7n)*7a-(–0,7n)*2,1+(–0,7n)*5k=-4,9na+1,47n=3,5nk;
_2_
1) 5х + 5у=5*(x+y);
2) 10аb + 3bc – b=b*(10a+3c-1);
3) 12mр – 16nр=4p*(3m-4n);
_3_
1) (x + 7,1) – (8,7 + х)=x + 7,1 – 8,7 - х=7,1 – 8,7= -(8,7-7,1)=-1,6;
2) –(7,3 – у) – (9,1 + у)= –7,3 + у – 9,1 - у=–7,3 – 9,1=-(7,3+9,1)=-16,4;
3) –(7,2 – m + k) + (5,3 + k)= –7,2 + m - k + 5,3 + k=–7,2 + m + 5,3 =m-(7,2-5,3)=m-1,9;
4) (b – с – 4,8) – (–с – b – 4,8)=b – с – 4,8 +с + b + 4,8=b + b =2b;
_4_
1) 7x – 18x – 19x + 21x=x(21-19-18+7)=x(9-18)=-x(18-9)=-9x;
2) –9у + 12у + 41y – 17y=y(12+41-17-9)=y(53-17-9)=27y;
3) 2,6а – 5,4b – а + 2b=a(2,6-1)-b(5,4-2)=1,6a-3,4b;
4) –5,6с + 4,8 + 8,2с – 9,1=c(8,2-5,6)-(9,1-4,8)=2,6c-4,3;
5) 4,6m + 8,3n – 5,1 – 8,3m – 6,4n=n(8,3-6,4)-m(8,3-4,6)-5,1=1,9n-3,7m-5,1;
6) –2a/3 + 5b/6 – a/8 – 7b/12=b/6(5-7/2)-a(2/3+1/8)=b/6(5-3,5)-a(2/3+1/8)=1,5b/6-19a/24=b/4-19a/24;
_5_
1) 9(7x – 6) – 18х=9*7x-9*6-18x=63x-18x-54=45x-54;
2) 7а – 6(19 – а)=7a-6*19+6*a=13a-114;
3) 0,8(6x – 2) + 1,6(х – 4)=0,8*6x-0,8*2+1,6*x-1,6*4=4,8x-1,6+1,6x-6,4=x(4,8+1,6)-(1,6+6,4)=6,4x-8;
4) 2,8(5b – 6а) – (7b – 8а) * 1,2=2,8*5b-2,8*6a-1,2*7b+1,2*8a=14b-16,8a-8,4b+9,6a=b(14-8,4)-a(16,8-9,6)=5,6b-7,2a;
5) –(–4,9 – 5,8с) – (3,1с – 5,6)=4,9 + 5,8с – 3,1с +5,6=c(5,8 – 3,1)+4,9+5,6=2,7c+10,5;
6) 8/9 * (2 1/4 * a – 3b/4) – 7/30 * (4 2/7 * a – 8 4/7 * b)=8/9 * (9/4 * a – 3b/4) – 7/30 * (30/7 * a – 60/7 * b)=2a – b*(2/3)– a + 2 b=a+b*(4/3);
_6_
6а – (3а – 9b),
а + 3b = –0,6.
6а – (3а – 9b)=6а – 3а + 9b=3a+9b=3*(a+3b)=3*(-0,6)=-1,8;
_7_
1) 0,6(4у – 18) – 0,4(5 – 7у)=2,4y-10,8-2+2,8y=5,2y-12,8 при у = 2 4/13;
y=2 4/13 =(26+4)/13=30/13
5,2*30/13-12,8=12-12,8=-0,8;
2) 5 1/4 * (12 – с) + 3 1/4 * (–с – 8) = (21/4)*12 -(21/4)c- (13/4)c- (13/4)*8=
=21*3 -(21/4)c- (13/4)c- 13*2 при с = –0,4.
63 -(21/4)*(-0,4)- (13/4)*(-0,4)- 26=37-(-0,4)(-34/4)=37-(34*0,4/4)=37-3,4=33,6