ответ: 15:2.
Объяснение:
Пусть х км/ч - скорость в стоячей воде, у км/ч - скорость течения реки, тогда (х+у)км/ч - скорость по течению, (х-у)км/ч -скорость против течения. Составим таблицу:
направление движения S км V км/ч t x
по течению реки 34 х+у 34/(х+у)
против течения 39 х-у 39/(х-у)
в стоячей воде 75 х 75/х
По условию задачи время движения по течению и против течения равно времени движения в стоячей воде.
Составим и решим уравнение:
34/(х+у)+39/(х-у)=75/х; Домножим обе части уравнеия на общий
знаменатель х(х+у)(х-у), одновременно
сокращая его со знаменателями дробей:
34х(х-у)+39х(х+у)=75(х²-у²);
34х²-34ху+39х²+39ху=75х²-75у²;
73х²+5ху-75х²+75у²=0;
-2х²+5ху+75у²=0; Разделим обе части уравнения на у²:
2 х²/у²-5 х/у-75=0; Пусть х/у=z, тогда:
2z²-5z-75=0;
D=25+4*2*75=25+600=625=25²;
z₁₂=(5±25):4;
z₁=15/2; z₂= -5 -не удовлетворяет смыслу задачи,т.к. z>0.
х/у=15/2 - отношение скорости движения в стоячей воде к скорости течения реки.
х - ширина прямоугольника
х + 8 - длина прямоугольника
(х + 8) * х = 65
х² + 8х - 65 = 0
Получили квадратное уравнение, ищем корни
х первое, второе = (-8 плюс минус √64+260) / 2
х первое, второе = (-8 плюс минус √324) / 2
х первое, второе = (-8 плюс минус 18) / 2
Отрицательный корень сразу отбрасываем, так как ширина не может быть отрицательной.
х = 5 это ширина прямоугольника (b)
5+ 8 = 13 это длина прямоугольника (а)
Р(периметр прямоугольника) = 2а + 2b
Подставляем, находим периметр
Р = 2 * 13 + 2 * 5 = 36 (см)
Верный ответ третий
Объяснение:
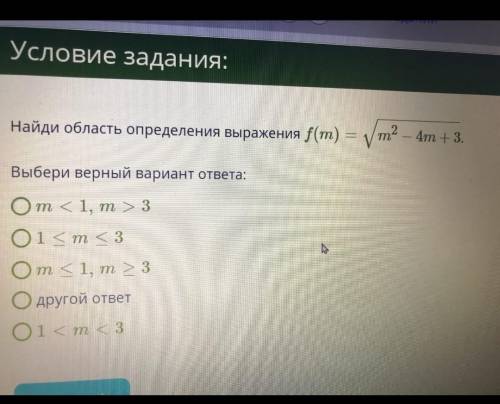
Выражение под корнем больше либо равно 0
Нам не подходит от 1 до 3
m >= 3
m <= 1