Нужно использовать следующие свойства числовых неравенств:
1. К обеим частям верного числового неравенства можно прибавить одно и то же число и получится верное числовое неравенство, т.е.:
если а < b и с - любое число, то a + c < b + c.
2. Обе части верного числового неравенства можно умножить (разделить) на одно и то же положительное число, при этом получиться верное числовое неравенство; если же число отрицательное, то знак неравенства изменится на противоположный, т.е.:
если а < b и с > 0, то ac < bc;
если а < b и с < 0, то ac >bc.
Таким образом, если а < b, то: 2,5а < 2,5b (2,5 > 0),
а затем и 2,5а - 7 < 2,5b - 7.
ответ: 2,5а - 7 < 2,5b - 7.
А) Точки пересечения с осями : (0, -2) и (5,0).
Б) Точка не принадлежит графику.
Объяснение:
А)
Функция х - 2,5 у - 5=0. имеет неприведенный вид. Для начала выразим у:
у =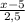 
Пересечение с осями определяется приравниванием х и у к нулю:
Если х = 0, то у = -2 график пересекает ось у
Если у = 0, то х = 5 график пересекает ось х
Точки пересечения с осями : (0, -2) и (5,0)
Б)
Чтобы проверить, принадлежит ли точка графику функции подставим вместо х --> -5,5 , а вместо у --> -2,6
-2,6 =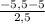 
выражение неверно , а значит точка не принадлежит графику.
Село - - - - - - - - - - - - - - - - - 95 км - - - - - - - - - - - - - - - - - - - Город
> х км/ч ? (х + 15) км/ч <
40 мин = 40/60 = 2/3 ч
1,5 ч = 90/60 = 3/2 ч
Уравнение:
х · (3/2 + 2/3) + (х + 15) · 2/3 = 95
3/2х + 2/3х + 2/3х + 30/3 = 95
9/6х + 4/6х + 4/6х + 10 = 95
17/6х = 95 - 10
17/6х = 85
х = 85 : 17/6
х = 85 · 6/17 = 5 · 6
х = 30 (км/ч) - скорость мотоцикла
30 + 15 = 45 (км/ч) - скорость автомобиля
ответ: 30 км/ч и 45 км/ч.
Проверка:
30 · (3/2 + 2/3) = 30 · 13/6 = 65 км проедет мотоцикл на 2 ч 10 мин
45 · 2/3 = 30 км - проедет автомобиль за 40 мин
65 + 30 = 95 км - расстояние от села до города