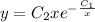г)Система уравнений не имеет решения.
д)Решение системы уравнений х=5,5
у=0
Система уравнений имеет одно решение.
Объяснение:
Выясните,имеет ли система решения и сколько:
г) х+ 2у = 3
у = -0,5х методом подстановки
у через х уже выражен во втором уравнении, подставим выражение в первое уравнение и вычислим х:
х+2(-0,5х)=3
х-х=3
0=3
Система уравнений не имеет решения.
д) 2х=11-2у
6у=22-4х
Разделим первое уравнение на 2 для удобства вычислений:
х=5,5-у
Подставим выражение х через у во второе уравнение и вычислим у:
6у=22-4(5,5-у )
6у=22-22+4у
6у-4у=0
у=0
х=5,5-у
х=5,5-0
х=5,5
Решение системы уравнений х=5,5
у=0
Система уравнений имеет одно решение.
Замена: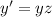
Подставляем в исходное уравнение:
Заметим, что - решение, так как обращает исходное уравнение в верное равенство. Если
- решение, так как обращает исходное уравнение в верное равенство. Если 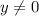 , то разделим обе части уравнения на
, то разделим обе части уравнения на 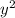 :
:
Замена: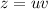
Подставляем в уравнение:
Предположим, что сумма первого и третьего слагаемого в левой части равна нулю. Тогда:
Тогда второе слагаемое левой части равно правой части уравнения:
Значит:
Далее получим:
Заметим, что частное решение , отмеченное ранее, получается при
, отмеченное ранее, получается при 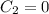 .
.
ответ: