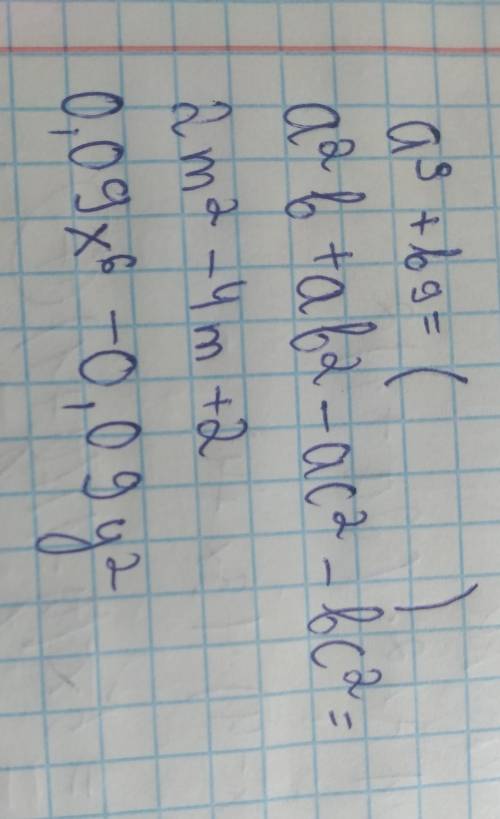
P=2(a+b)P=2(a+b)
S=a*bS=a∗b
Подставим вместо S и Р известные значения, и объединим эти два уравнения в систему:
\left \{ {{28=2(a+b)} \atop {48=a*b }} \right.{
48=a∗b
28=2(a+b)
\left \{ {{14=a+b} \atop {48=a*b }} \right.{
48=a∗b
14=a+b
\left \{ {{a=14-b} \atop {48=a*b }} \right.{
48=a∗b
a=14−b
Первое уравнение будет являться подстановкой,заменим им а во втором уравнении:
48=b*(14-b)48=b∗(14−b)
48=14b-b^248=14b−b
2
b^2-14b+48=0b
2
−14b+48=0
По т. Виета
b_1=6, b_2=8b
1
=6,b
2
=8
Подставим в подстановку вместо b;
a_1=14-6=8a
1
=14−6=8
a_2=14-8=6a
2
=14−8=6
Длины сторон нашего прямоугольника 8см и 6см
переходи по ссылке там ответ
Ну или не переходи
Решите систему неравенств:
x²-3x+9>0
x²≤36
Решить первое неравенство:
x² - 3x + 9 > 0
Приравнять к нулю и решить квадратное уравнение:
x² - 3x + 9 = 0
D=b²-4ac =9 - 36 = -27
D < 0
Уравнение не имеет действительных корней.
Значит, неравенство выполняется всегда или не выполняется никогда.
Подставить в неравенство произвольное значение х:
х = 0;
0 - 0 + 6 > 0, выполняется.
Значит, неравенство верно при любом значении х.
Решение первого неравенства: х∈(-∞; +∞).
Решить второе неравенство:
x² ≤ 36
Приравнять к нулю и решить квадратное уравнение:
x² = 36 неполное квадратное уравнение
х = ±√36
х₁ = -6;
х₂ = 6.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -6 и х= 6.
Решение второго неравенства: х∈[-6; 6].
Неравенство нестрогое, скобки квадратные.
Отметить на числовой оси интервалы решений двух неравенств и найти пересечение решений, это будет решение системы неравенств.
Пересечение решений: х∈[-6; 6].