Если P(x) делится на Q(x), то
P(x)/Q(x)=A(x) ,где A(x)-многочлен.
Поскольку Q(x) делится на P(x),то
Q(x)/P(x)=B(x) ,где B(x) -многочлен.
Откуда верно, что:
A(x)*B(x)=1
Если знаете комплексный анализ, то очевидно, что многочлен со степенью больше нуля имеет хотя бы один корень (комплексный или действительный),но тогда и произведение многочленов должно иметь этот корень,но многочлен C(x)=A(x)*B(x)=1 ,не может иметь корней тк 1 не равно 0.
А значит оба многочлена A(x) и B(x) имеют нулевую степень (константы),таким образом B(x)=c.(с не равно 0)
Q(x)=c*P(x)
Пусть многочлен A(x) имеет степень n ,а многочлен B(x) имеет степень m.Тогда очевидно, что многочлен A(x)*B(x) имеет степень m+n, но 1 это многочлен нулевой степени:
m+n=0
Тк m>=0 и n>=0, то m=n=0.
То есть B(x)=c (с не равно 0)
Q(x)=c*P(x) ,что и требовалось доказать.
ответ: 931
Объяснение:
1. Заметим, что 315 имеет следующее разложение на простые множители:
315=32⋅5⋅7,
отсюда следует, что числа x, y, z состоят из тех же простых чисел 3, 5, 7:
x=3a1⋅5a2⋅7a3;
y=3b1⋅5b2⋅7b3;
z=3c1⋅5c2⋅7c3.
При этом
0≤a1,b1,c1≤2;
0≤a2,b2,c2≤1;
0≤a3,b3,c3≤1.
2. По правилу нахождения наименьшего общего кратного получим
НОК(3a1⋅5a2⋅7a3;3b1⋅5b2⋅7b3;3c1⋅5c2⋅7c3)=3max(a1,b1,c1)⋅5max(a2,b2,c2)⋅7max(a3,b3,c3).
3. Итак, задача свелась к нахождению числа решений системы уравнений:
⎧⎩⎨⎪⎪max(a1,b1,c1)=2;max(a2,b2,c2)=1;max(a3,b3,c3)=1.
Так как каждое уравнение содержит разные неизвестные, то для того чтобы найти количество решений системы, нужно найти количество решений каждого из уравнений и перемножить полученные значения.
4. Начнём с первого уравнения. Требуется найти количество целых неотрицательных чисел a1,b1,c1, удовлетворяющих уравнению max(a1,b1,c1)=2.
Напомним, что 0≤a1,b1,c1≤2. Отсюда следует, что тройка чисел a1,b1,c1 является решением уравнения, если хотя бы одно из чисел a1,b1,c1 равно 2. Для того чтобы посчитать число таких троек, вычтем из количества всевозможных троек чисел a1,b1,c1 с условием 0≤a1,b1,c1≤2 (таких троек ровно 33=27 штук) число троек a1,b1,c1 с условием 0≤a1,b1,c1≤2, в которых 2 ни разу не встречается (таких троек ровно 23=8 штук). Отсюда находим, что первое уравнение системы имеет 27−8=19 решений.
5. Точно так же поступим при подсчёте числа решений второго уравнения системы. Требуется найти количество целых неотрицательных чисел a2,b2,c2, удовлетворяющих уравнению max(a2,b2,c3)=1.
Напомним, что 0≤a2,b2,c2≤1.
Тройка чисел a2,b2,c2 является решением уравнения, если хотя бы одно из чисел a2,b2,c2 равно 1. Но только одна тройка чисел a2,b2,c2 не удовлетворяет этому условию, это тройка a2=b2=c3=0. Все остальные тройки хотя бы одну 1 содержат. Поскольку троек чисел a2,b2,c2 с условием 0≤a2,b2,c2≤1 ровно 23=8 штук, то второе уравнение системы имеет 8−1=7 решений. Точно так же получаем, что и третье уравнение системы имеет 7 решений.
6. Для того чтобы подсчитать число решений системы, а значит, и исходного уравнения, остаётся перемножить полученные нами числа. Имеем
19⋅7⋅7=931.
Итак, исходное уравнение имеет ровно 931 решение.
Правильный ответ: 931 решение.
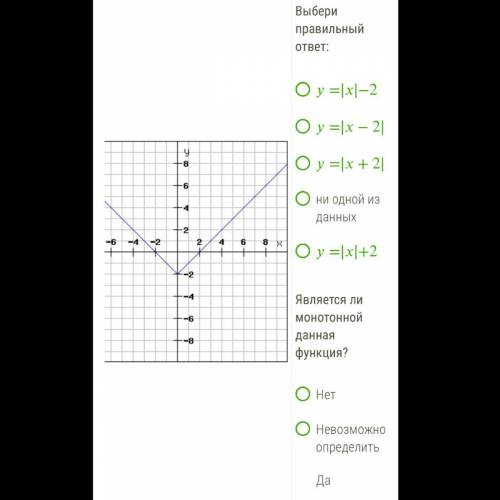
1) y = |x|-2
2) Нет
Объяснение:
1) Так как функция принимает отрицательные значения, то варианты 2 и 3 сразу отпадают, во варианте ответа 4 наша функция по оси y сместилась на 2 единицы вверх, а у нас она наоборот, относительно 0, сместилась на две единицы вниз, поэтому ответ: y = |x|-2
2) Нет, т.к. вначале наша функция убывает до x=0, а затем начинает возрастать