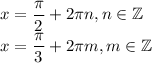
Объяснение:
Запоминаем, что tg x > 0, и возводим в квадрат:
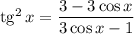
По известной формуле тангенс в квадрате выражается через косинус:
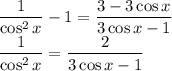
При следующем переходе возникают ограничения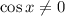 
, 
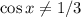. Если они выполнены, то можно всё домножить на знаменатели "крест накрест":
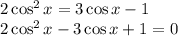
Получилось уравнение, сводящееся к квадратному относительно косинуса. Один корень угадывается - это cos x = 1, второй по теореме Виета cos x = 1/2. Дальше остаётся решить эти уравнения и учесть ограничения (фактически остается отобрать решения, удовлетворяющие неравенству tg x > 0).
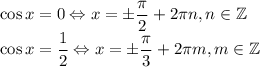
Не удовлетворяют условию tg x > 0 серии решений, которые соответствуют выбору "-".
решение на фотографии.