Искомая функция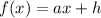 
.
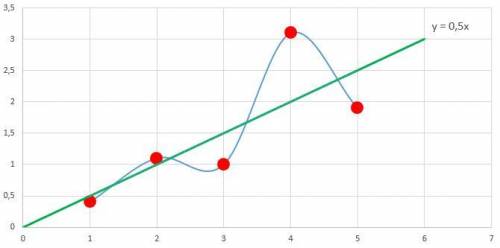
Найдем значения искомой функции в заданных точках х:
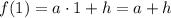
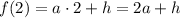
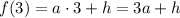
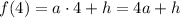
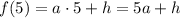
Кроме этого, для каждого из аргументов х есть еще и экспериментальное значение, которое обозначим через функцию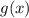 
:
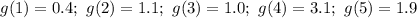
Составим функцию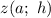 
, которая будет суммировать квадраты разностей значений функций 
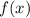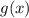и соответствующих аргументов:
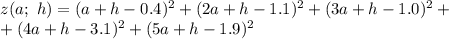
Исследуем эту функцию на экстремумы.
Найдем частные производные:
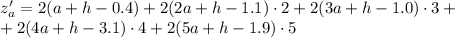
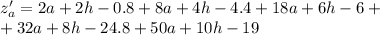
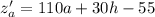
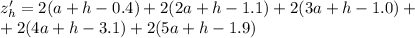
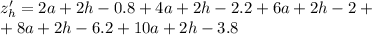
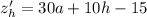
Необходимое условие экстремума - равенство нулю частных производных. Составим систему:
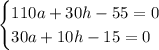
Домножим второе уравнение на (-3):
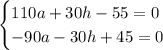
Складываем уравнения:
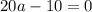
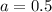
Подставим значение а во второе уравнение исходной системы:
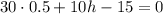
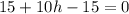
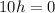
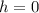
Точка (0.5; 0) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
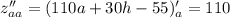
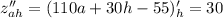
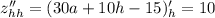
Рассмотрим выражение:
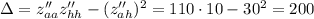
Так как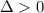 
и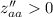 
, то точка (0.5; 0) является точкой минимума.
Значит, в точке (0.5; 0) функция 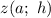имеет минимум.
Тогда, значения 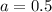и 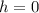есть искомые коэффициенты функции .
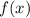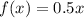
ответ: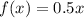
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
