Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
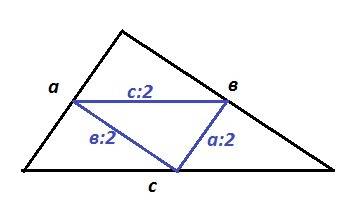
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.
Решаем уравнение:
3/6y - 9 = - 12 + y/6;
Переносим известное в правую часть равенства, неизвестное в левую, меняя знаки на противоположные:
3/6y - y/6 = - 12 + 9;
3/6y - y/6 = - 3;
Избавляемся от знаменателя, умножив на его значение обе части уравнения:
3y - y = - 18;
Приводим подобные слагаемые:
2y = - 18;
Делим обе части уравнения на число при переменной:
y = - 18 / 2;
y = - 9;
Проверяем:
3/6 х (- 9) - 9 = - 12 + (- 9)/6;
- 9/2 - 9 = - 12 - 1,5;
- 4,5 - 9 = - 13,5.