ответ Г
Пояснение:
чем больше отнимают от числа, тем меньше оно становится. То же самое и со сложением - чем больше прибавляют, тем больше число
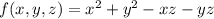
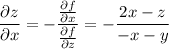
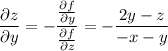
 с координатами
с координатами 
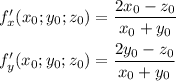
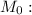
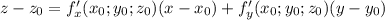 - уравнение касательной в общем виде.
- уравнение касательной в общем виде.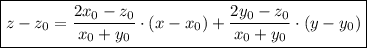 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  с координатами
с координатами 
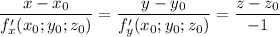
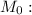
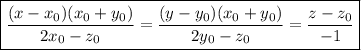 - каноническое уравнение нормали к поверхности в точке
- каноническое уравнение нормали к поверхности в точке  с координатами
с координатами 
Г. x − 3; x − 0,5; x; x + 1; x + 1,5.
Обьяснение: Пусть х - 1, тогда
Г. -2; 0,5; 1; 2; 2,5