И известно, что для того, чтобы купить машину первый из них работал 20 месяцев (и заработал рублей). А второй работал 8 месяцев (заработал: ). И при этом оба смогут купить одну и ту же машину, то есть количество полученных ими денег одинаковое. Поэтому мы можем составить и решить уравнение:
Получается, что Иванов получает за месяц 10000 рублей. Тогда Петров получает 25000. И машина стоит:
X - первоначальная загрузка первой машины y - первоначальная загрузка второй машины n - первоначальное количество рейсов n*x -n*y =60 или n(x-y)=60 ---> (x-y) =60/n
(x-4) последующая загрузка первой машины (y-3) последующая загрузка второй машины (n+10) последующее количество рейсов (n+10)(x-4 -y+3) =60 (n+10)(x-y-1) =60 ( n+10)(x-y) -(n+10) =60 (x-y) -1=60/(n+10) (x-y)= 60/(n+10) +1 и ранее: х -y =60/n 60/(n+10) +1= 60/n 60n+n²+10n=60n+600 n²+10n-600=0 D=2500 n1=(-10+50)/2=20 n2<0 не уд.усл. (первоначальное количество рейсов n =20) выполненное количество рейсов n+10=30
n(x-y) =60 x-y=60 : 20 x-y =3 первоначальная разность загрузки первой и второй машины (x>4 y>3) x-y=2 - реальная разность загрузок машин (конкретно загрузку каждой машины определить невозможно, так как не дано ни общее количество перевозимого груза, ни грузоподъёмность машин и не оговорена допустимая загрузка машин).
Пусть Иванов получает за месяц
рублей.
Тогда Петров получает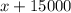
рублей.
И известно, что для того, чтобы купить машину первый из них работал 20 месяцев (и заработал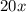
рублей). А второй работал 8 месяцев (заработал: 
). И при этом оба смогут купить одну и ту же машину, то есть количество полученных ими денег одинаковое. Поэтому мы можем составить и решить уравнение:
Получается, что Иванов получает за месяц 10000 рублей. Тогда Петров получает 25000. И машина стоит:
10000 * 20 = 200000 (рублей)
Задача решена!