Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
б) y= график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: то х∈(-∞;-7)∪(-7;+∞) Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево. Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
, (1вариант) х∈(-∞;-7)∪(-7;+∞) или (2 вариант) D=(-∞;-7)∪(-7;+∞)
1. Аргумент = 2, это означает, что х = 2. Подставим это значение в функцию и получим её значение. y = 8*2 - 3 = 16 - 3 = 13
При х = 2, у = 13
2. Значение функции = -19, это означает, что у = -19. Подставим это значение функции и найдем аргумент: -19 = 8x - 3 -8х = -3 + 19 -8х = 16 |:(-8) x = -2
При у = -19, х = -2
3. Чтобы определить, принадлежит ли точка графику функции, необходимо подставить значения её координат в функцию. Если получится верное числовое равенство, то точка принадлежит графику.
В(-2.-13) -13 = 8 * (-2) - 3 -13 = -16 - 3 -13 = -19 - неверно, поэтому точка В не принадлежит графику функции. В(-2.-13) ∉ y = 8x - 3
y=1+x3, х∈(-∞;+∞) или D=(-∞;+∞)
y=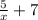 , х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
, х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
Объяснение:
Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
б) y=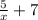 график гиберболы х∈(-∞;0)∪(0;+∞)
график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: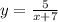 то х∈(-∞;-7)∪(-7;+∞)
то х∈(-∞;-7)∪(-7;+∞)
Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево.
Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=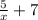 , (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)