
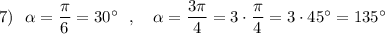
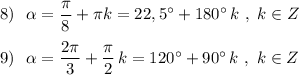
Все 4 функции вида y = kx + b. если b > 0, то прямая соприкасается с осью ординат выше оси абсцисс, а если b < 0, то прямая соприкасается с осью ординат ниже оси абсцисс.
Значит, графики A и B соответствуют уравнениям 2 и 3, а графики C и D соответствуют уравнениям 1 и 4. Определим теперь конкретно какой график к какому уравнению подходит.
Рассмотрим уравнение, в котором k = 2
y = 2x + 5, причём x = = 2,5. Значит, прямая проходит через точку абсцисс 2,5.
Рассмотрим уравнение, в котором k = 1
y = x - 5, из свойств числового коэффициента b следует, что график проходит через точку ординат -5, а из формулы y = a(x - m)² следует, что точка соприкосновения оси абсцисс и прямой смещена вправо на 5.
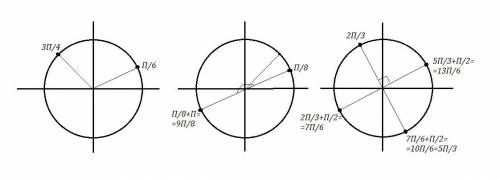
Проведя аналогичные рассуждения с остальными двумя уравнениями и их графиками, придём к выводу, что
1) - C
2) - A
3) - B
4) - D
В решении.
Объяснение:
Коммунальным работникам нужно разбить на аллее клумбу квадратной формы со стороной а м. Найдите длину стороны клумбы (в м), если при увеличении ее на 2 м площадь клумбы увеличится на 148 м².
а - длина стороны клумбы первоначальная.
а² - площадь клумбы первоначальная.
(а + 2) - длина стороны клумбы увеличенная.
(а + 2)² - площадь клумбы увеличенная.
По условию задачи уравнение:
(а + 2)² - а² = 148
Раскрыть скобки:
а² + 4а + 4 - а² = 148
Привести подобные члены:
4а = 144
а = 144/4
а = 36 (м) - длина стороны клумбы первоначальная.
36 + 2 = 38 (м) - длина стороны клумбы увеличенная.
Проверка:
36² = 1296 (м²);
38² = 1444 (м²).
1444 - 1296 = 148 (м²), верно.