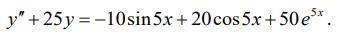
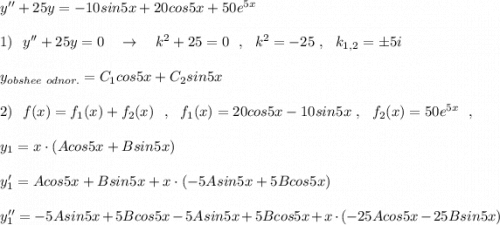
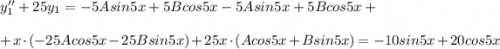
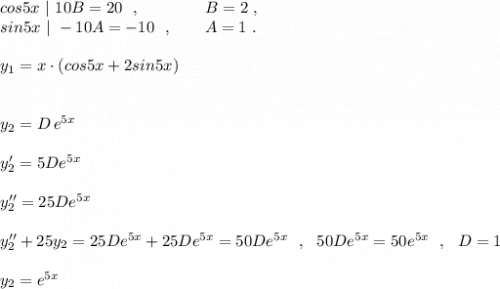
y=x^2-3x+2
1) Находим точки пересечения графика функции с осью Ох:
х^2-3x+2=0
x1=1, x2=2
(1;0) и (2;0) - искомые точки
2) Находим уравнение касательной к графику функции в точке х=1
y`(x)=(x^2-3x+2)`=2x-3
y`(1)=2*1-3=-1 k1=-1
y(1)=1^2-3*1+2=1-3+2=0
y=0+(-1)(x-1)=-x+1 -уравнение касательной в точке х=1
3) Находим уравнение касательной к графику функции в точке х=2
y`(2)=2*2-3=4-3=1 k2=1
y(2)=2^2-3*2+2=4-6+2=0
y=0+1(x-2)=x-2 -уравнение касательной в точке х=2
4) Коэффициент угла наклона первой касательной k1=-1, а второй касательной k2=1,
следовательно, касательные взаимно перпендикулярны,
т.е.угол между ними равен 90 градусов.