Question

Числовая окружность. Кто может пояснить почему мы берём именно 3 углов прямых и добавляем их к сумме , и как их найти?, если считать без калькулятора возможно их найти самому, объясните как?.

Answer 1

Так как при вращении на 360°=2П радиан , мы попадаем в ту же точку ,

то угол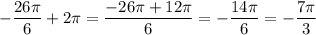    $-\dfrac{26\pi }{6}+2\pi =\dfrac{-26\pi +12\pi }{6}=-\dfrac{14\pi }{6}=-\dfrac{7\pi }{3}$    попадает в ту же

точку на единичной окружности , что и угол (-26П/6) .

Но угол (-7П/3)  не лежит между 0 и 2П . Поэтому надо прибавить не 2П,

а  больше , чтобы попасть в промежуток [ 0 ; 2П ] . Подбираем число n .

Если прибавить 3*2П , то получим  

$-\dfrac{26\pi }{6}+3\cdot 2\pi =\dfrac{-26\pi +36\pi }{6}=\dfrac{10\pi }{6}=\dfrac{5\pi }{3}=300^\circ\ \ ,\ \ \ \ \dfrac{5\pi }{3}\in [\ 0\ ;\ 2\pi \ ]$

Полученный угол  принадлежит промежутку [ 0; 2П ] .

Замечание.  Если прибавить 2*2П , то не получим угол из

промежутка [ 0;2П ] . Действительно,

$-\dfrac{26\pi }{6}+2\cdot 2\pi =\dfrac{-26\pi +24\pi }{6}=\dfrac{-2\pi }{6}=-\dfrac{\pi }{3}$  .

То есть можно сообразить, что в числитель к (-26П) надо прибавить число, большее 26П, чтобы получить положительный угол. И соответственно подбирать n .

Если прибавить 4*2П , то получим угол, который больше, чем 2П. Действительно,

$-\dfrac{26\pi }{6}+4\cdot 2\pi =\dfrac{-26\pi +48\pi }{6}=\dfrac{22\pi }{6}=\dfrac{11\pi }{3}=660^\circ 360^\circ$

То есть n=2 и n=4 не подходит , а n=3 как раз подходит .