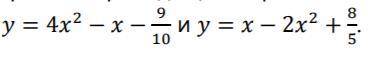
Будем считать, что задано уравнение: 4 – 5cos7x – 2sin²7x = 0.
Заменим 2sin²7x = 2(1 - cos²7x):
4 – 5cos7x – 2(1 - cos²7x) = 0. Заменим cos7x = t и получим квадратное уравнение: 2 - 5t + 2t² = 0.
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:
D=(-5)^2-4*2*2=25-4*2*2=25-8*2=25-16=9;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√9-(-5))/(2*2)=(3-(-5))/(2*2)=(3+5)/(2*2)=8/(2*2)=8/4=2 (нет по ОДЗ;
t_2=(-√9-(-5))/(2*2)=(-3-(-5))/(2*2)=(-3+5)/(2*2)=2/(2*2)=2/4=1/2.
Обратная замена: cos7x = 1/2.
7х = 2πk +- (π/3), k ∈ Z.
ответ: х = (2/7)πk +- (π/21), k ∈ Z.
В точках пересечения значения функций совпадают, значит, можно определить координаты точек, приравняв уравнения.
4x² - x - (9/10) = -2x² + x + (8/5).
Получаем квадратное уравнение 6x² - 2x - (25/10) = 0.
Ищем дискриминант:
D=(-2)^2-4*6*(-2.5)=4-4*6*(-2.5)=4-24*(-2.5)=4-(-24*2.5)=4-(-60)=4+60=64;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√64-(-2))/(2*6)=(8-(-2))/(2*6)=(8+2)/(2*6)=10/(2*6)=10/12=5/6~~0.83333;
x_2=(-√64-(-2))/(2*6)=(-8-(-2))/(2*6)=(-8+2)/(2*6)=-6/(2*6)=-6/12=-0.5.
Находим значения "у".
y1 = -2*(25/36) + (5/6) + (8/5) = 94/15,
y2 = -2*(1/4) + (-1/2) + (8/5) = 3/5.
Имеем две точки А((5/6); (94/15)) и В(-1/2); (3/5)).
Вектор ВА = ((5/6)-(-1/2); ((94/15)-(3/5)) = (8/6); 85/15) = ((4/3); (17/3)).
Уравнение прямой через две точки пересечения:
(x - (5/6))/94/3) = (y - (94/15))/(17/3).