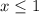ответ: хЄ (- ∞ ; 1 ] .
Объяснение:
( x - 1 )| x² + 1 | + | x - 1 |( x² + 1 ) = 0 ;
( x - 1 )( x² + 1 ) + | x - 1 |( x² + 1 ) = 0 ;
( x² + 1 )( x - 1 + | x - 1 | ) = 0 ;
x² + 1 ≠ 0 або x - 1 + | x - 1 | = 0 ;
розв"язуємо останнє рівняння :
| x - 1 | = - х + 1 ;
вираз під модулем дорівнює 0 при х = 1 .
1) х ≤ 1 , тоді - ( x - 1 ) = - ( x - 1 ) ; правильна рівність при хЄ (- ∞ ; 1 ] ;
2) x > 1 , тоді x - 1 = - х + 1 ; > 2x = 2 ; > x = 1 ∉ ( 1 ; + ∞ ) .
В - дь : хЄ (- ∞ ; 1 ] .
В решении.
Объяснение:
Сначала нужно раскрыть скобки, потом привести подобные члены, потом перенести неизвестное влево, известное вправо и вычислить неизвестную величину.
1) (3y-1)-(2y+4)+y=33
3у-1-2у-4+у = 33
2у = 33+5
2у=38
у=38/2
y= 19;
2) 15x=(6x-1)-(x+18)
15х = 6х-1-х-18
15х-5х = -19
10х = -19
х= -19/10
х= -1,9;
3) 17p-8-(p+7)+15p=0
17p-8-p-7+15p=0
31p = 15
p=15/31;
4) (6m-4)-(7m+7)-m=1
6m-4-7m-7-m = 1
-2m = 1+11
-2m = 12
m= 12/-2
m= -6.
Проверка путём подстановки вычисленных значений х, у, p и m в уравнения показала, что данные решения удовлетворяют данным уравнениям.
а) 1
б) 1
Объяснение:
Касательной к графику функции у (х) является первая производная у', значение которой в точке x₀ равно тангенсу угла между касательной к графику функции у (х) и осью х.
а)
1) Находим производную:
y' = (х⁶ - 4х)' = (х⁶)' - (4х)' = 5x⁵ -4
2) Находим значение производной y' = 5x⁵- 4 в точке x₀ = 1:
y'(1) = 5x⁵ -4 = 5 · 1⁵ - 4 = 5 - 4 = 1
ответ: 1
б)
1) Находим производную:
y' = (√х - 3)' = (√х)' - (3)' = 1/(2√x) - 0 = 1/(2√x)
2) Находим значение производной y' = 1/(2√x) в точке x₀ = 1/4:
y' (1/4) = 1/(2√x) = 1/ (2 · 1/2) = 1/1 = 1
ответ: 1
Объяснение:
х²+1 всегда больше нуля, значит просто опускаем модуль
Объединяем:
ответ: