Смотри, ученика всего 23. У нас спрашивают, что сколько учеников имеет ТОЧНО более трёх конфет.
Нам сказано, что 7 из них имеют по 3 или менее конфет, а восемнадцать, по 2 или больше. А всего учеников-то 23!
2 или больше, может быть те восемнадцать имеют 3 конфеты, значит они входят в те 7. (ведь 7 учеников получили 3 или меньше, а 18 2 или больше, они могли получить 3 конфеты, ведь 2>3)
23-7=16 (конфет, которые ещё входят в список возможных детей, у которых больше 3-ёх конфет)
Но, ведь 18+7=25! А не 23, значит те, кто входят в число 18-ть (эти 2 человека из тех семи, кто имеет меньше двух конфет) Значит 2 человека ещё выпадают, у них по 3 или менее конфет. (Ведь нам не сказано, что 18 имеют по 3 или более, нам сказано, что 18 имеют 2 и более, значит могут иметь и 3 конфетки, и входить в число тех, кто получил меньше трёх, а не больше)
Значит 16-2=14 (ещё минус 2 человека)
Это число тех, кто точно имеет больше трёх конфет.
ответ: 14
M(0,5;1,5)
Объяснение:
M(x;y)=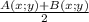
M(0,5;1,5)