x ∈{-2} ∪ [2;7]
Объяснение:
1) Найдём нули функции у₁ = х²-5х-14:
х²-5х-14 = 0
х₁,₂ = 5/2 ± √(25/4 +14) = 5/2 ± √(81/4) = 5/2 ± 9/2
х₁ = 5/2 + 9/2 = 14/2 = 7
х₂ = 5/2 - 9/2 = - 4/2 = -2
Графиком функции у₁ = х²-5х-14 является парабола, ветви которой направлены вверх; следовательно, у₁ = х²-5х-14 ≤0 на участке
x ∈ [-2; 7].
2) Неравенство х² ≥ 4 эквивалентно неравенству: х²- 4 ≥ 0.
Найдём нули функции у₂ =х²- 4:
х²- 4 = 0
х² = 4
х = ± √4
х₃ = - 2
х₄ = 2
Графиком функции у₂ = х²- 4 является парабола, ветви которой направлены вверх; функция у₂ = х²- 4 больше или равна нулю на участках:
x ∈(-∞; -2] ∪ [2;+∞)
3) Объединяем полученные решения, для чего на числовой оси отмечаем точки х₂ = -2; х₃ = -2; х₄ = 2; х₁ = 7 и находим перекрываемые области значений, одновременно удовлетворяющие неравенству х²-5х-14 ≤ 0 и неравенству х² ≥ 4:
x ∈{-2} ∪ [2;7]
ответ: x ∈{-2} ∪ [2;7]
1. (a-5)²+(a+7)(a-7)+8a=
=a²-10a+25+a²-49+8a =
=2a²-2a-24 = а² -а-12
2. a) 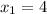
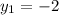
б) 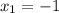
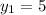
4. а) 2a(a^2-64)= 2a(a-8)(a+8)
б) a(5-b) - b(5-b)= (a-b)(5-b)
5. х деталей за 1 час по плану.
Уравнение :
(х+4)*8=10х
х=16
16*10=160
6. Обозначим ОА=х, а ОВ=у, и составим систему уравнений, исходя из условия задачи
х+у = 17
у-х = 1
Из второго ур-я выразим у и подставим во втрое ур-е
у = 1+х
х+х+1 = 17
2х = 17-1=16
х = 8 см
х= ОА = 8 см, а оа иесть расстояние от точки до прямой.
ответ: расстояние равно 8 см
ответ ниже
Объяснение:
В первых двух примерах просто делим на 60, так как в минуте 60 секунд.
А где 180 см/с, переводим сантиметры в метры.
54 м/мин = 0.9 м/с
108 м/мин = 1.8 м/с
180 см/с = 1.8 м/с