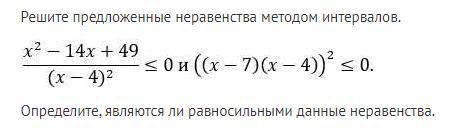
Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение:
1а) скобка у=1-7х
4х-у=32
4х+1+7х=32
4х+7х=32+1
11х=33х=33/11
х=3
у=1-7*3
у= - 20
1б) скобка х=у+2
3х-2у=9
3*(у+2)-2у=9
3у+6-2у=9
3у-2у=9-6
у=3
х=3+2
х=5
2а) скобка 5х-3у=14 скобка 5х-3у=14
2х+у=10 у=10-2х
5х-3*(10-2х)=14
5х-30+6х=14
5х+6х=14+30
11х=44
х=44/11
х=4
у=10-2*4
у=2
2б) скобка х+5у=35 скобка х=35-5у
3х+2у=27 3х+2у=27
3*(35-5у)+2у=27
105-15у+2у=27
-13у=27-105
-13у=-78
13у=78
у=78/13
у=6
х=35-5*6
х=5
3а) скобка 2х-у=2 скобка - у=2-2х скобка у= - 2+2х
3х-2у=3 3х-2у=3 3х-2у=3
3х-2*( - 2+2х)=3
3х+4-4х=3
3х-4х=3-4
- х=-1
х=1
у= - 2+2*1
у=0
3б) скобка 5у-х=6 скобка - х=6-5у скобка х= - 6+5у
3х-4у=4 3х-4у=4 3х-4у=4
3*( - 6+5у)-4у=4
- 18+15у-4у=4
11у=4+18
у=22/11
у=2
х= - 6+5*2
х= - 6+10
х=4
1) (x-4)^2=0 ; x=4
( при чем (x-4)^2 всегда >0)
x^2-14x+49=0
(x-7)^2=0 ; x=7
(при чем здесь (x-7)^2 не может быть <0, а только =0)
Значит чтобы неравенство было верно - подходит только один корень
x=7
2) выражение ((x-7)(x-4))^2 не может быть <0, тогда
x-7=0
x1=7
и
x-4=0
x2=4
Объяснение:
я написал это в 22:15, так что у тебя еще есть время