
9.
log₁₄ 7 = m найдем log₁₇₅ 56 - ?
log₁₄ 5 = n
Используем формулу перехода другому основанию:
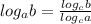
log₁₇₅ 56 = log₁₄ 56/log₁₄ 175 = log₁₄ (8×7)/log₁₄ (25×7) = log₁₄ (2³×7)/log₁₄ (5²×7) = log₁₄ 2³ × log₁₄ 7/log₁₄ 5² × log₁₄ 7 = 3log₁₄ 2 × log₁₄ 7/2log₁₄ 5 × log₁₄ 7
Нам нужно найти log₁₄ 2:
log₁₄ 2 = log₁₄ 14/7 = log₁₄ 14 - log₁₄ 7 = 1 - m
Получаем:
log₁₇₅ 56 = 3×(1 - m) + m/2n + m = 3 - 3m + m/2n + m = 3 - 2m/2n + m
ответ: log₁₇₅ 56 = 3 - 2m/2n + m
10.
log₅ 5 = 1
log₁₁ 15 = log₁₀ 15/log₁₀ 11 ≈ 1,17609/1,04139 ≈ 1,12934
Следовательно:
1 < 1,12934
log₅ 5 < log₁₁ 15
ответ: log₅ 5 < log₁₁ 15
Объяснение:
1. Элементы множества могут быть перечислены в любом порядке.
1) {1/5; 2/5; 3/5; 4/5}
2) {ф; и; з; к; а}
3) {1; 2; 3; 0}
2. Пересечение и объединение множеств.
A = {1; 2; 3; 4; 6; 12}
B = {1; 2; 4; 8; 16}
Пересечение: {1; 2; 4}
Объединение: {1; 2; 3; 4; 6; 8; 12; 16}
3. Сравнить числа:
1) 5,(16) и 5,16
5,(16) = 5,1616...
5,16 = 5,1600...
5,(16) > 5,16
2) -2,(35) и -2,5
-2,(35) = -2,3535...
-2,5 = -2,5000...
2,5 > 2,3535..., у отрицательных чисел все наоборот поэтому:
-2,(35) > -2,5
3) 6,(23) и 6,24
6,(23) = 6,2323...
6,24 = 6,2400...
6,(23) < 6,24
4. И 5. Задания повторяют 1. И 2.
............................................