1) прировняем к нулю:
-х^2+3х=0
Х(-х+3)=0
Х=0 и - х=-3
Х=3
Критические точки- 0и 3.
2) обозначим их на координатой прямой:
~~>
0. 3
Где ~- закрашенная точка.
3) теперь будем брать любые числа из промежутков и подставлять в уравнение. Если получится положительное число, то ставим +, если отрицательное, то -.
А) возьмём - 1( самый первый--левый промежуток)
Получим - (-1)^2-3= - 1-3=-4. Будет знак -
Б) возьмём из второго промежутка число 1.
-(1)^2+3= - 1+3=2. ЗНАК +
В) ВОЗЬМЁМ 10 ИЗ ТРЕТЬЕГО промежутка.
-(10)^2+30= - 100+30=-70 знак -.
4) получим:
- +. -
~~>
0. 3
У нас в неравенстве знак больше или равно, значит нас интересуют промежутки, которые со знаком плюс. Неравенство не строгое (или равно), значит скобки квадратные в ответе.
Наш промежуток с плюсом пойдёт в
ответ: [0;3]
Парабола – график квадратичной функции. Этот график позволяет прослеживать основные свойства функции в зависимости от вида квадратичной функции.
Существуют различные преобразования графиков, если тебе нужно узнать поподробнее об этом напиши в комментариях и я объясню.
Мы рассмотрим только все самое основное.
В функции y= a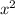
От коэффициента а зависит то куда направлены ветви параболы и то, как они идут.
Если коэффициент а>0, тогда ветви будут идти вверх.
Если коэффициент а<0, тогда ветви будут идти вниз.
От этого коэффициента и зависит то, как они выглядят.
Если коэффициент больше 1, то парабола будет идти резче вверх, а то, насколько он больше 1 будет показателем того насколько она идет резче по оси оу.
Если коэффициент больше 0, но меньше 1, то парабола будет более прижатой к оси абсцисс (ох), а коэффициент будет показателем того насколько она прижата к оси.
Для этого на примере рассмотрим графики функций у=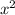 , у=2
, у=2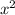 и у=
и у=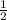
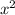
Заранее прощения не за самые ровные графики.
На этом графике мы видим подтверждение ранее сказанного правила.
По функции можно сразу определять каким будет график параболы.