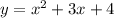
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
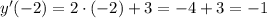
Уравнение касательной имеет вид:
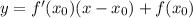
Подставим значение 
Итак, уравнение касательной заданной функции: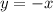 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
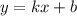численно равен тангенсу угла наклона 
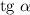с положительным направлением оси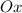 
В найденной касательной коэффициент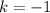 
, следовательно, 
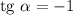при 
или 
ответ: или
Аналогично: sin 4п=0, сos4П =1
sin3,5п=1, сos3,5П=0;
sin5/2П=1, cos 5/2П=0
sinПк=0 сosПк=1 (если к -четное ) и cosПк =-1 если к- нечетное число
(2к+1) - это формула нечетного числа, к примеру 3, 5, 7, 9 и т.д.
Следовательно, sin(2к+1)П=0, cos(2к+1)П =-1..