x∈(-∞; -1,5]
Объяснение:
Даны
h(x) = -2·x+1, g(x) = 3·x+3.
Определим вид h(g(x)), то есть :
h(g(x)) = h(3·x+3) = -2·(3·x+3)+1 = -6·x-6+1= -6·x-5.
Составим и решаем заданное неравенство h(g(x))≥h(x):
-6·x-5 ≥ -2·x+1
-6·x+2·x ≥ 1+5
-4·x ≥ 6 | :(-4)
x ≤ -6/4
x ≤ -1,5
x∈(-∞; -1,5].
х дней - требуется первой бригаде
у дней - второй бригаде
х-у=10
1/х + 1/у=1/12
.
х=10+у
12(у+х)=ху
.
х=10+у
12(у+10+у)=у(10+у)
.
х=10+у
24у+120=10у+у²
.
х=10+у
у² - 14у - 120=0
D/4=7²+120=169 (±13²)
у1=7-13= - 6 - не подходит решению
у2=7+13=20
.
у=20
х=10+у
.
у=20(дней) - потребуется второй бригаде
х=30(дней) - потребуется первой бригаде
или
1/х (часть) - делает первая бригада за 1 день
1/(х-10) (часть) - делает вторая за 1 день
1/12 (часть) - делают вместе за 1 день
.
1/х + 1/(х-10) =1/12
12(х-10+х)=х(х-10)
24х - 120=х² - 10х
х² - 34х+120=0
D/4=17²-120=169 (±13²)
х1=17-13=4 - не подходит решению
х2=17+13=30(дн.) - потребуется первой
30-10=20(дн.) - потребуется второй
(-∞; -1,5]
Объяснение:
Надо решить неравенство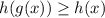
Составим данное неравенство
Тогда получим неравенство
x∈(-∞; -1,5]