***
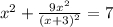 =>
=> 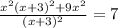 =>
=> 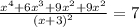
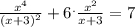
пусть:
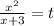
используя теорему Виета
находим t1 и t2
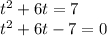
=>
t₁ = -7
t₂ = 1
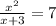 =>
=> 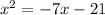 =>
=> 
находим дискриминант уравнения х² + 7х + 21 = 0
D = b² - 4ac = 49 - 4 · 1 · 21 = 49 - 84 = - 35 < 0
поскольку дискриминант отрицательный, значит уравнения не имеет решений
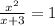 =>
=> 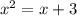 =>
=> 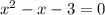
находим дискриминант уравнения х² - х - 3 = 0
D = b² - 4ac = (-1)² - 4 · 1 · (-3) = 13
X₁ = (-b + √D) / 2 = (1 + √13) / 2X₂ = (-b - √D) / 2 = (1 - √13) / 2ответ: X₁ = (-b + √D) / 2 = (1 + √13) / 2
X₂ = (-b - √D) / 2 = (1 - √13) / 2
√(х+3) >√(2х-1)+ √(х-1).
2)D(f)
{x+3≥ 0,
{2x-1≥ 0,
{x-1≥0. Общее решение данной системы x≥ 1.
1) Возводим обе части в квадрат , тк левая и правые части положительны
х+3>2х-1+2√(2х-1)*√(х-1)+х-1,
5-2х>2√(2х²-3х+1). После возведения в квадрат получаем
25-20х+4 х²> 8х²-12х+4,
4х² +8х-21<0.
3)Нули функции f=4х² +8х-21.
4х² +8х-21=0 ,D=400, x1=1,5 , x2=-3,5.
Тогда 4(х-1,5)(х+3,5)<0
4)Найдем знаки функции на [1;+беск).
Значение -3,5∉[1;+беск).
4(х-1,5)(х+3,5)<0
[1] - - - - [1,5]+ + +
Определим знак последнего интервала f(2)=4*2²+8*2-21=11>0. На этом интервале ставим знак «+».
5) ответ. [1;1,5]
ответ:1) х≥0 2) х≥3 если я правильно понял задание(моя рідна мова—Українська)
Объяснение: