x^3 + 3x^2 - 4
В разложении на скобки стоят корни многочлена.
Первым делом нужно угадать хотя бы один корень (есть еще вариант для нахождения корней многочлена 3й степени с формулы, но она крайне громоздкая, вряд ли у Вас расчет на нее, если хотите, можете загуглить).
Например, есть теорема, что любой рациональный корень многочлена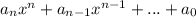 
представим в виде дроби 
, где p - делитель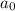 
и q - делитель 
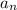. В данном случае 
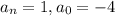, следовательно рациональными корнями могут быть только 1, -1, 2, -2, 4, -4.
Проверяем 1
1 + 3 - 4 = 0. Верно, значит 1 - корень
Вообще, можно и так глядя на многочлен, заметить, что 1 - корень
Теперь делим многочлен на (x - 1) (это по теореме Бизу). С процесс деления показать не могу, но должно получиться x^3 + 3x^2 - 4 = (x-1)(x^2 + 4x + 4)
Многочлен (x^2 + 4x + 4) = (x+2)^2, т.к. это квадрат суммы.
Получаем x^3 + 3x^2 - 4 = (x-1)(x^2 +4x +4) = (x-1)(x+2)^2
Надеюсь
a) пересечение (5;9); обьединение (2;5)U(5;9)U(9;12)
б) пересечение [-7;10];обьединение [-10;12]
в) пересечение (-4;6 ); обьединение [-7;-4] U (4;6)U(6;8 ]
г) пересечение (8;+бесконечность)
обьединение (5;8)U (8;+бесконечность)
д) пересечение (-бесконечность; 10)
обьединение (-бесконечность; 10)U(10;12)
е) пересечение (7;11)
обьединение (-бесконечность ;7)U(7;11)U(11;+бесконечность)
последний вариант правильный