
![a) \frac{2}{ \sqrt[4]{3} } = \frac{2}{ \sqrt[4]{3} } * \frac{ \sqrt[4]{3 {}^{3} } }{ \sqrt[4]{3 {}^{3} } } = \frac{2 \sqrt[4]{27} }{ \sqrt[4]{3*3 {}^{3} } } = \frac{2 \sqrt[4]{27} }{ \sqrt[4]{3 {}^{4} } } = \frac{2 \sqrt[4]{27} }{3}](/tpl/images/2055/5463/7379a.png)
![b) \frac{2}{ \sqrt[3]{5} - 1 } = \frac{2}{ \sqrt[3]{5} - 1 } * \frac{ \sqrt[3]{25} + \sqrt[3]{5} + 1}{ \sqrt[3]{25} + \sqrt[3]{5} +1 } = \frac{2( \sqrt[3]{25} + \sqrt[3]{5} + 1) }{( \sqrt[3]{5} - 1)*( \sqrt[3]{25} + \sqrt[3]{5} + 1)} = \frac{2( \sqrt[3]{25} + \sqrt[3]{5} + 1) }{5 - 1} = \frac{2( \sqrt[3]{25} + \sqrt[3]{5} + 1) }{4} = \frac{ \sqrt[3]{25} + \sqrt[3]{5} + 1}{2}](/tpl/images/2055/5463/d8316.png)
Объяснение:
![\displaystyle\frac{2}{\sqrt[4]{3} }\cdot\frac{\sqrt[4]{3^3} }{\sqrt[4]{3^3}} = \frac{2\sqrt[4]{27} }{3} \\\\\\\frac{2}{\sqrt[3]{5}-1 } \cdot\frac{\sqrt[3]{5^2} +\sqrt[3]{5}+1 }{\sqrt[3]{5^2} +\sqrt[3]{5}+1} =\frac{2(\sqrt[3]{5^2} +\sqrt[3]{5}+1)}{(\sqrt[3]{5})^3-1^3} =\\\\\\=\frac{2(\sqrt[3]{5^2} +\sqrt[3]{5}+1)}{4} =\frac{\sqrt[3]{25} +\sqrt[3]{5}+1}{2}](/tpl/images/2055/5463/c5c2a.png)
ответ: скорость катера по течению 15 км/час
Объяснение:
Пусть собственная скорость катера х (км/час),
тогда скорость движения ПО течению будет (х+3) км/час - течение реки "несет" катер, увеличивая скорость движения; даже плот (не имея двигателя, т.е. его собственная скорость =0)) движется по течению реки (со скоростью течения))
в озере вода не течет (течения нет), скорость движения будет равна собственной скорости катера.
S (км) = V (км/час) * t (час)
5 (км) = (х+3) * t1 ---> t1 (час) = 5 / (x+3) ---это время движения по течению реки
8 (км) = х * t2 ---> t2 (час) = 8 / x ---это время движения по озеру
все время (сумма) = 1 час
уравнение: 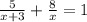
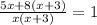
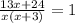
x² + 3x = 13x + 24
x² - 10x - 24 = 0; по т.Виета корни (12) и (-2)
скорость не может быть отрицательным числом, ---> x=12 (км/час)
ПРОВЕРКА:
по озеру катер идет со скоростью 12 км/час, время в пути 8/12 часа = 2/3 часа = 40 минут
по течению реки катер идет со скоростью (12+3) км/час, время в пути 5/15 часа = 1/3 часа = 20 минут
20 минут + 40 минут = 60 минут = 1 час.
ответ: скорость катера по течению 15 км/час
Объяснение:
Пусть собственная скорость катера х (км/час),
тогда скорость движения ПО течению будет (х+3) км/час - течение реки "несет" катер, увеличивая скорость движения; даже плот (не имея двигателя, т.е. его собственная скорость =0)) движется по течению реки (со скоростью течения))
в озере вода не течет (течения нет), скорость движения будет равна собственной скорости катера.
S (км) = V (км/час) * t (час)
5 (км) = (х+3) * t1 ---> t1 (час) = 5 / (x+3) ---это время движения по течению реки
8 (км) = х * t2 ---> t2 (час) = 8 / x ---это время движения по озеру
все время (сумма) = 1 час
уравнение: 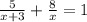
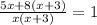
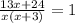
x² + 3x = 13x + 24
x² - 10x - 24 = 0; по т.Виета корни (12) и (-2)
скорость не может быть отрицательным числом, ---> x=12 (км/час)
ПРОВЕРКА:
по озеру катер идет со скоростью 12 км/час, время в пути 8/12 часа = 2/3 часа = 40 минут
по течению реки катер идет со скоростью (12+3) км/час, время в пути 5/15 часа = 1/3 часа = 20 минут
20 минут + 40 минут = 60 минут = 1 час.